623. 在二叉树中增加一行

题目描述：

给定一个二叉树的根 root 和两个整数 val 和 depth ，在给定的深度 depth 处添加一个值为 val 的节点行。

注意，根节点 root 位于深度 1 。

加法规则如下:

• 给定整数 depth，对于深度为 depth - 1 的每个非空树节点 cur ，创建两个值为 val 的树节点作为 cur 的左子树根和右子树根。
• cur 原来的左子树应该是新的左子树根的左子树。
• cur 原来的右子树应该是新的右子树根的右子树。
• 如果 depth == 1 意味着 depth - 1 根本没有深度，那么创建一个树节点，值 val 作为整个原始树的新根，而原始树就是新根的左子树。

测试用例：

示例 1:

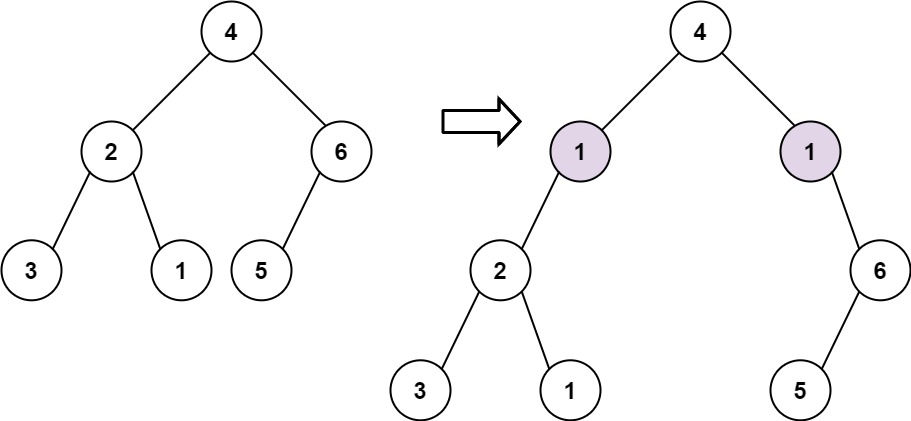
输入: root = [4,2,6,3,1,5], val = 1, depth = 2
输出: [4,1,1,2,null,null,6,3,1,5]

示例 2：

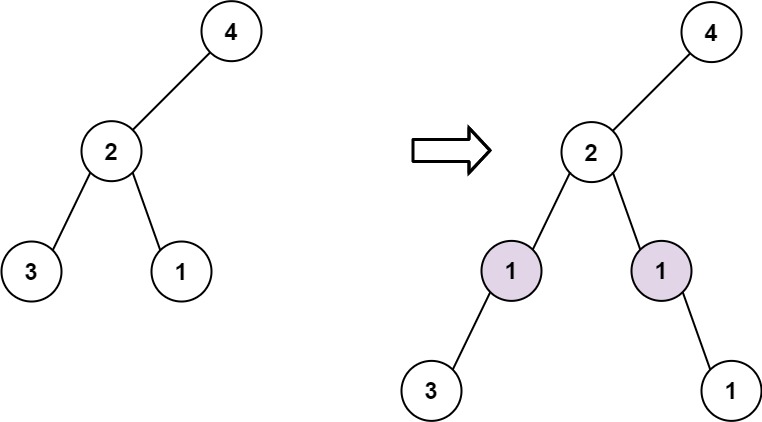
输入: root = [4,2,null,3,1], val = 1, depth = 3
输出: [4,2,null,1,1,3,null,null,1]

限制及提示：

• 节点数在 [1, 10^4] 范围内
• 树的深度在 [1, 10^4]范围内
• -100 <= Node.val <= 100
• -10^5 <= val <= 10^5
• 1 <= depth <= the depth of tree + 1

---

解题分析及思路：

本题可以采用二叉树 🔗的层级遍历来解答

遍历每一层，直到遍历到需要更改的层数。

因为最开始就已经将root加进去，并且是depth - 1行，所以当depth > 2即可跳出循环。循环结束后，队列里保存的就是需要增加子节点的节点

queue := []*TreeNode{root}
for depth > 2 {
    l := len(queue)
    for index := 0; index < l; index++ {
        node := queue[index]
        if node != nil {
            queue = append(queue, node.Left)
            queue = append(queue, node.Right)
        }
    }
    queue = queue[l:]
    depth--
}

遍历数组，为每一个节点增加子节点，增加左节点及右节点，并将其左节点的左节点指向原来的左节点，将其右节点的右节点指向原来的右节点即可。

l := len(queue)
for index := 0; index < l; index++ {
    node := queue[index]
    if node != nil {
        node.Left = &TreeNode{
            Val:  val,
            Left: node.Left,
        }
        node.Right = &TreeNode{
            Val:   val,
            Right: node.Right,
        }
    }
}

当然，本题也可以使用深度优先搜索。

复杂度：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

执行结果：

• 执行耗时:4 ms,击败了82.67% 的Go用户
• 内存消耗:5.8 MB,击败了10.67% 的Go用户