2192. 有向无环图中一个节点的所有祖先

题目描述：

给你一个正整数 n ，它表示一个 有向无环图 中节点的数目，节点编号为 0 到 n - 1 （包括两者）。

给你一个二维整数数组 edges ，其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。

请你返回一个数组 answer，其中 answer[i]是第 i 个节点的所有 祖先 ，这些祖先节点 升序 排序。

如果 u 通过一系列边，能够到达 v ，那么我们称节点 u 是节点 v 的 祖先 节点。

示例 1：

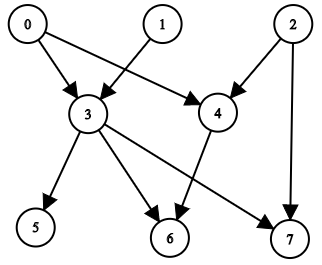
输入：n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
输出：[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
解释：
上图为输入所对应的图。
- 节点 0 ，1 和 2 没有任何祖先。
- 节点 3 有 2 个祖先 0 和 1 。
- 节点 4 有 2 个祖先 0 和 2 。
- 节点 5 有 3 个祖先 0 ，1 和 3 。
- 节点 6 有 5 个祖先 0 ，1 ，2 ，3 和 4 。
- 节点 7 有 4 个祖先 0 ，1 ，2 和 3 。

示例 2：

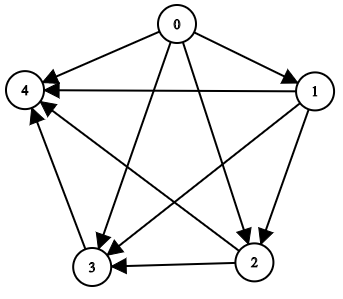
输入：n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
输出：[[],[0],[0,1],[0,1,2],[0,1,2,3]]
解释：
上图为输入所对应的图。
- 节点 0 没有任何祖先。
- 节点 1 有 1 个祖先 0 。
- 节点 2 有 2 个祖先 0 和 1 。
- 节点 3 有 3 个祖先 0 ，1 和 2 。
- 节点 4 有 4 个祖先 0 ，1 ，2 和 3 。

提示：

• 1 <= n <= 1000
• 0 <= edges.length <= min(2000, n * (n - 1) / 2)
• edges[i].length == 2
• 0 <= from_i, to_i <= n - 1
• from_i != to_i
• 图中不会有重边。
• 图是 有向 且 无环 的。

---

解题分析及思路：

方法：深度优先遍历

题解CopyRight：灵茶山艾府 🔗

思路：

例如示例 1，从 2 出发 DFS，可以访问到 4,6,7 那么把 2 加到 answer[4],answer[6],answer[7] 中。

依次从起点 start=0,1,2,…,n−1 出发 DFS，途中把 start 加到能访问到的点的 answer 中。由于 start 从小到大枚举，所以 answer[i] 列表自然就是有序的了。

例如：

• 从 000 出发访问到 5，把 0 加到 answer[5] 中，现在 answer[5]=[0]。
• 从 111 出发访问到 5，把 1 加到 answer[5] 中，现在 answer[5]=[0,1]。
• 从 333 出发访问到 5，把 3 加到 answer[5] 中，现在 answer[5]=[0,1,3]。

小技巧：无需每次 DFS 前都重新初始化 vis 数组。我们会跑 n 个 DFS，每个 DFS 的 start 都是不同的。利用这一条件，当访问到节点 x 时，标记 vis[x]=start，表示 x 是本轮 DFS 中访问到的节点。当我们访问到某个节点 y 时，如果发现 vis[y]=start，就表示 y 访问过了，否则没有访问过。

注：本题输入的是一个有向无环图，但该方法并不需要这个条件，即使图中有环，我们也可以找到所有能访问到 i 的节点。

func getAncestors(n int, edges [][]int) [][]int {
	g := make([][]int, n)
	for index := range edges {
		g[edges[index][0]] = append(g[edges[index][0]], edges[index][1])
	}
	var result = make([][]int, n)
	vis := make([]int, n)
	start := 0
	var appendResultFunc func(key int)
	appendResultFunc = func(key int) {
		vis[key] = start + 1 // 避免重复访问
		for _, v := range g[key] {
			if vis[v] != start+1 {
				result[v] = append(result[v], start)
				appendResultFunc(v)
			}
		}
	}
	for ; start < n; start++ {
		appendResultFunc(start) // 从 start 开始 DFS
	}
	return result
}

复杂度：

• 时间复杂度：O(N * (N + M))，其中 m 是 edges 的长度。对于每个起点 start，跑一次 DFS 的时间复杂度为 O(N + M)。

• 空间复杂度：O(N + M)

执行结果：

• 执行用时：118 ms, 在所有 Go 提交中击败了64.71%的用户
• 内存消耗：21.15 MB, 在所有 Go 提交中击败了70.%的用户