1252. 奇数值单元格的数目

题目描述：

给你一个 m x n 的矩阵，最开始的时候，每个单元格中的值都是 0。

另有一个二维索引数组 indices，indices[i] = [ri, ci] 指向矩阵中的某个位置，其中 ri 和 ci 分别表示指定的行和列（从 0 开始编号）。

对 indices[i] 所指向的每个位置，应同时执行下述增量操作：

• ri 行上的所有单元格，加 1 。
• ci 列上的所有单元格，加 1 。
• 给你 m、n 和 indices 。请你在执行完所有 indices 指定的增量操作后，返回矩阵中 奇数值单元格 的数目。

测试用例：

示例 1:

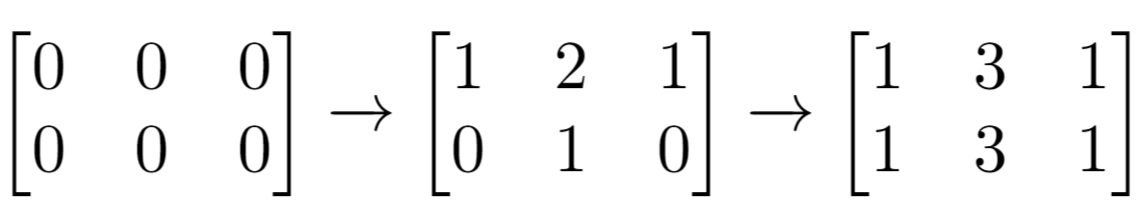
输入：m = 2, n = 3, indices = [[0,1],[1,1]]
输出：6
解释：最开始的矩阵是 [[0,0,0],[0,0,0]]。
第一次增量操作后得到 [[1,2,1],[0,1,0]]。
最后的矩阵是 [[1,3,1],[1,3,1]]，里面有 6 个奇数。

示例 2:

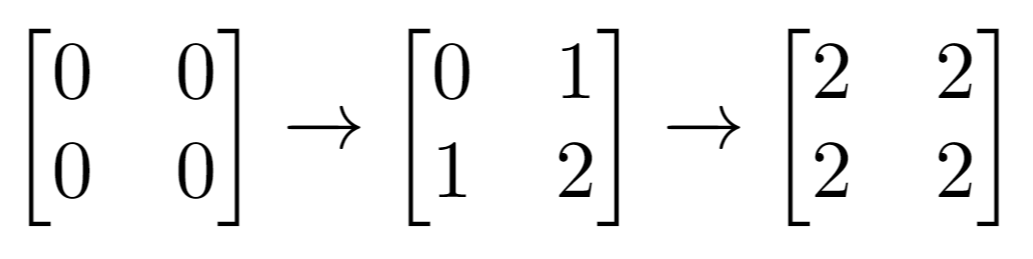
输入：m = 2, n = 2, indices = [[1,1],[0,0]]
输出：0
解释：最后的矩阵是 [[2,2],[2,2]]，里面没有奇数。

限制及提示：

• 1 <= m, n <= 50
• 1 <= indices.length <= 100
• 0 <= ri < m
• 0 <= ci < n

---

解题分析及思路：

由于这一题数据量比较小，那么直接暴力模拟直接接可以A掉这道题。

那么有什么方法可以优化一下呢？

根据题目我们可以得知，对于m * n 的二维数组在位置[row,col]的的值是等于该行row增加的数与该列col增加的数的总和，所以我们只需统计每一行和每一列增加的数，然后最后再对某一个位置进行计算即可。

统计时，我们只需判断该位置的值是不是奇数即可。

为了优化计算速度，我们可以把需要计算的位置换成位计算。

代码分析：

定义行、列数组分别保存该行需要增加的数和该列需要增加的数。

rows := make([]int, m)
cols := make([]int, n)
for index := range indices {
    rows[indices[index][0]]++
    cols[indices[index][1]]++
}

通过统计某一位置的值（row + col）是否为奇数即可。

for _, row := range rows {
    for _, col := range cols {
        ans += (row + col) % 2
    }
}

计算换成位计算。

rows := make([]int, m)
cols := make([]int, n)
for index := range indices {
    rows[indices[index][0]] ^= 1
    cols[indices[index][1]] ^= 1
}

for _, row := range rows {
    for _, col := range cols {
        ans += (row + col) & 1
    }
}

复杂度：

• 时间复杂度：O(m * n)
• 空间复杂度：O(m + n)

执行结果：

• 执行用时：0 ms, 在所有 Go 提交中击败了100.00%的用户
• 内存消耗：2.3 MB, 在所有 Go 提交中击败了90.91%的用户