133. 克隆图

题目描述：

给你无向 连通 🔗 图中一个节点的引用，请你返回该图的 深拷贝 🔗（克隆）。

图中的每个节点都包含它的值 val（ int） 和其邻居的列表（ list[Node]）。

class Node {
    public int val;
    public List<Node> neighbors;
}

测试用例格式：

简单起见，每个节点的值都和它的索引相同。例如，第一个节点值为 1（ val = 1），第二个节点值为 2（ val = 2），以此类推。该图在测试用例中使用邻接列表表示。

邻接列表 是用于表示有限图的无序列表的集合。每个列表都描述了图中节点的邻居集。

给定节点将始终是图中的第一个节点（值为 1）。你必须将 给定节点的拷贝 作为对克隆图的引用返回。

示例 1：

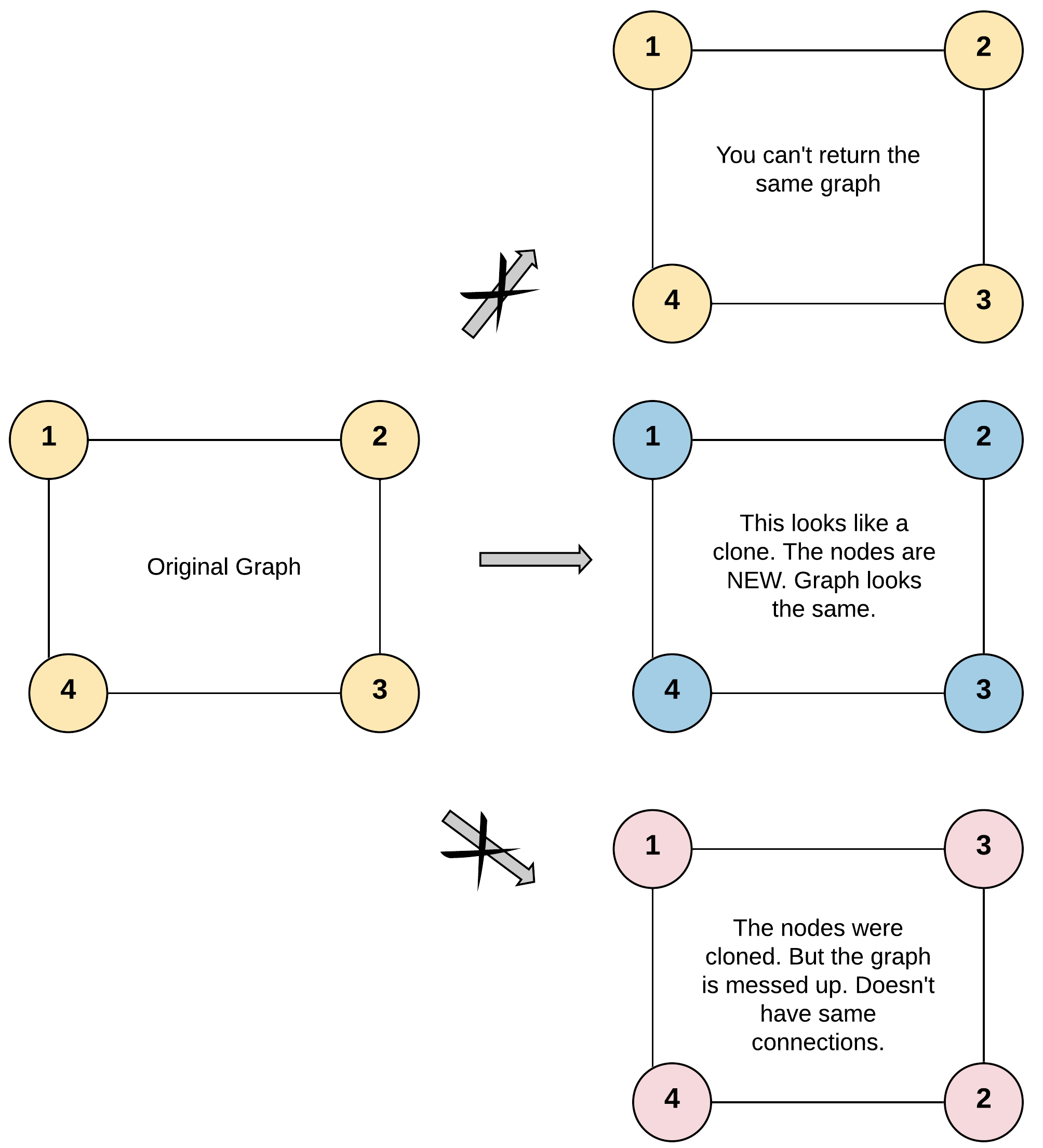
输入：adjList = [[2,4],[1,3],[2,4],[1,3]]
输出：[[2,4],[1,3],[2,4],[1,3]]
解释：
图中有 4 个节点。
节点 1 的值是 1，它有两个邻居：节点 2 和 4 。
节点 2 的值是 2，它有两个邻居：节点 1 和 3 。
节点 3 的值是 3，它有两个邻居：节点 2 和 4 。
节点 4 的值是 4，它有两个邻居：节点 1 和 3 。

示例 2：

输入：adjList = [[]]
输出：[[]]
解释：输入包含一个空列表。该图仅仅只有一个值为 1 的节点，它没有任何邻居。

示例 3：

输入：adjList = []
输出：[]
解释：这个图是空的，它不含任何节点。

提示：

• 这张图中的节点数在 [0, 100] 之间。
• 1 <= Node.val <= 100
• 每个节点值 Node.val 都是唯一的，
• 图中没有重复的边，也没有自环。
• 图是连通图，你可以从给定节点访问到所有节点。

---

解题分析及思路：

方法：深度优先搜索（DFS）+ 哈希表映射

思路：

克隆图的核心挑战是：

1. 确保每个节点只被克隆一次（避免重复创建）；
2. 正确复制节点间的连接关系（邻居列表需指向克隆后的节点，而非原图节点）。

算法的核心思路是深度优先搜索（DFS）+ 哈希表映射：

• 哈希表（map）：存储 “原图节点值 → 克隆节点” 的映射，用于快速判断节点是否已被克隆，同时作为克隆节点的 “缓存”。
• DFS 遍历：从起始节点出发，递归遍历所有可达节点。对于每个节点：
  • 若已克隆（存在于哈希表中），直接返回克隆节点；
  • 若未克隆，先创建克隆节点并存入哈希表，再递归克隆其所有邻居，构建克隆节点的邻居列表。

步骤 1：初始化哈希表

创建一个 map[int]*Node 类型的哈希表 m，键为原节点的 Val，值为对应的克隆节点。利用节点值唯一的特性，通过 Val 快速定位已克隆的节点。

步骤 2：DFS 递归克隆节点

• 终止条件：若当前节点为 nil，直接返回 nil；若当前节点已被克隆（存在于哈希表中），返回哈希表中对应的克隆节点（避免重复克隆）。
• 克隆当前节点：若节点未被克隆，创建新节点（复制 Val），并将其存入哈希表。
• 递归克隆邻居：遍历原节点的所有邻居，递归调用 DFS 克隆每个邻居，将克隆结果加入新节点的 Neighbors 列表，建立邻居关系。

步骤 3：返回克隆结果

从初始节点开始 DFS，最终返回克隆图的对应节点。

func cloneGraph(node *Node) *Node {
	var m = make(map[int]*Node)
	var dfs func(node *Node) *Node
	dfs = func(node *Node) *Node {
		if node == nil {
			return nil
		}
		if n, ok := m[node.Val]; ok {
			return n
		}
		n := &Node{Val: node.Val}
		m[node.Val] = n
		for index := range node.Neighbors {
			n.Neighbors = append(n.Neighbors, dfs(node.Neighbors[index]))
		}
		return n
	}
	return dfs(node)
}

复杂度：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

执行结果：

• 执行耗时:0 ms,击败了100.00% 的Go用户
• 内存消耗:4.6 MB,击败了30.88% 的Go用户