3070. 元素和小于等于 k 的子矩阵的数目

题目描述：

给你一个下标从 0 开始的整数矩阵 grid 和一个整数 k。

返回包含 grid 左上角元素、元素和小于或等于 k 的 子矩阵 的数目。

示例 1：

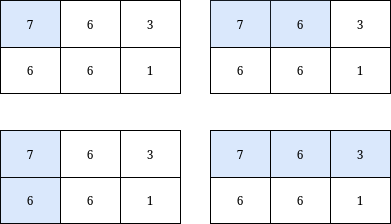
输入：grid = [[7,6,3],[6,6,1]], k = 18
输出：4
解释：如上图所示，只有 4 个子矩阵满足：包含 grid 的左上角元素，并且元素和小于或等于 18 。

示例 2：

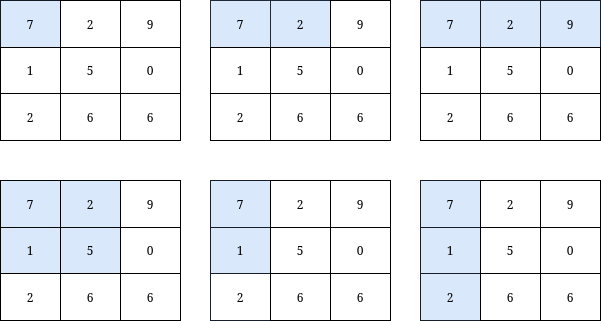
输入：grid = [[7,2,9],[1,5,0],[2,6,6]], k = 20
输出：6
解释：如上图所示，只有 6 个子矩阵满足：包含 grid 的左上角元素，并且元素和小于或等于 20 。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= n, m <= 1000
• 0 <= grid[i][j] <= 1000
• 1 <= k <= 10^9

---

解题分析及思路：

方法：前缀和

思路：

使用前缀和数组 dp 记录每个位置的前缀和，dp[i][j] 表示以 (i, j) 为右下角的子矩阵的元素和。

针对位置 (i, j) 的子矩阵，从 (0, 0) 到 (i, j) 的和可以通过 dp[i][j] = grid[i][j] - dp[i][j-1] - dp[i-1][j] + dp[i-1][j-1] 计算出子矩阵的元素和。

然后遍历 dp 数组，统计元素和小于或等于 k 的子矩阵的数目。

func countSubmatrices(grid [][]int, k int) int {
	var dp = make([][]int, len(grid))
	l := len(grid[0])
	dp[0] = make([]int, l)
	for i := 0; i < l; i++ {
		if i == 0 {
			dp[0][i] = grid[0][i]
		} else {
			dp[0][i] = grid[0][i] + dp[0][i-1]
		}
	}
	for i := 1; i < len(grid); i++ {
		dp[i] = make([]int, l)
		for j := range grid[i] {
			if j == 0 {
				dp[i][j] = grid[i][j] + dp[i-1][j]
			} else {
				dp[i][j] = grid[i][j] + dp[i-1][j] + dp[i][j-1] - dp[i-1][j-1]
			}
		}
	}
	var count int
	for i := range dp {
		for j := range dp[i] {
			if dp[i][j] <= k {
				count++
			}
		}
	}
	return count
}

复杂度：

• 时间复杂度：O(M * N)，其中 M 和 N 分别为 grid 的行数和列数
• 空间复杂度：O(M * N)

执行结果：

• 执行耗时:183 ms,击败了89.70% 的Go用户
• 内存消耗:24.4 MB,击败了72.73% 的Go用户