2673. 使二叉树所有路径值相等的最小代价

题目描述：

给你一个整数 n 表示一棵 满二叉树 里面节点的数目，节点编号从 1 到 n 。根节点编号为 1 ，树中每个非叶子节点 i 都有两个孩子，分别是左孩子 2 * i 和右孩子 2 * i + 1 。

树中每个节点都有一个值，用下标从 0 开始、长度为 n 的整数数组 cost 表示，其中 cost[i] 是第 i + 1 个节点的值。每次操作，你可以将树中 任意 节点的值 增加 1 。你可以执行操作 任意 次。

你的目标是让根到每一个 叶子结点 的路径值相等。请你返回 最少 需要执行增加操作多少次。

注意：

• 满二叉树 指的是一棵树，它满足树中除了叶子节点外每个节点都恰好有 2 个子节点，且所有叶子节点距离根节点距离相同。
• 路径值 指的是路径上所有节点的值之和。

示例 1：

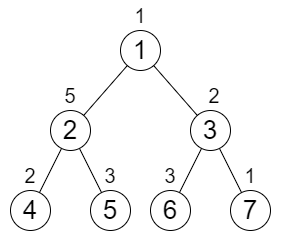
输入：n = 7, cost = [1,5,2,2,3,3,1]
输出：6
解释：我们执行以下的增加操作：
- 将节点 4 的值增加一次。
- 将节点 3 的值增加三次。
- 将节点 7 的值增加两次。
从根到叶子的每一条路径值都为 9 。
总共增加次数为 1 + 3 + 2 = 6 。
这是最小的答案。

示例 2：

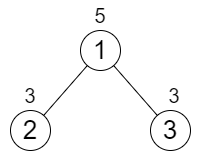
输入：n = 3, cost = [5,3,3]
输出：0
解释：两条路径已经有相等的路径值，所以不需要执行任何增加操作。

提示：

• 3 <= n <= 10^5
• n + 1 是 2 的幂
• cost.length == n
• 1 <= cost[i] <= 10^4

---

解题分析及思路：

方法：贪心

对于一个根节点 node，如果想要经过他到达叶子节点，那么node节点的左右节点的值必须相等，否则就需要增加操作。

我们可以从叶子节点开始，向上递归，每次递归都将当前节点的值增加到与其父节点的值相等，直到根节点。

以该树为例：

• 如果需要从根节点 1 经过 2 ，到达 4 和 5 的路径和相等，那么 4 的值必须 增加 1 次 ，使得 4 的值为 3，同时将 4 和 5 的父亲节点的值增加 3，值为 8
• 同理，如果需要从根节点 1 经过 3 ，到达 6 和 7 的路径和相等，那么 7 的值必须 增加 2 次 ，使得 7 的值为 3，同时将 6 和 7 的父亲节点的值增加 3，值为 5
• 此时，从节点 2 达到 4 和 5 的路径和相等，不需要增加操作，从节点 3 到达 6 和 7 的路径和相等，不需要增加操作
• 但是从根节点 1 到达 2 和 3 的路径和不想等，同样的操作需要将 3 的值 增加 3 次 ，使得 3 的值为 8
• 整个过程，增加了六次操作

那为什么不从上累积到下呢？

因为从下到上的话，每次都需要将父节点的值增加到与其子节点的值相等，这样会导致重复增加操作。

那为什么不层级遍历到最大值，并将每层的节点与最大值的差值累加呢？

因为层级遍历，会增加不需要增加的次数。

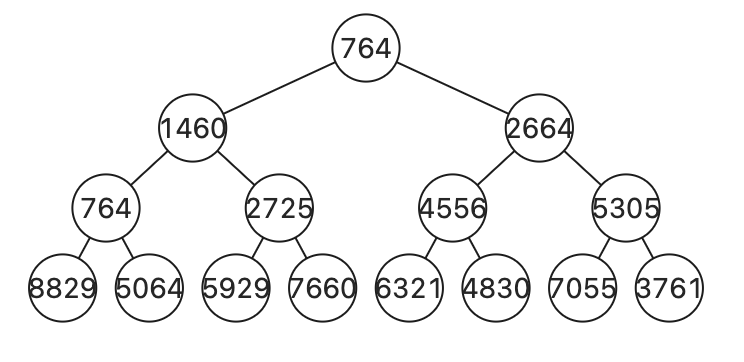
例如[764, 1460, 2664, 764, 2725, 4556, 5305, 8829, 5064, 5929, 7660, 6321, 4830, 7055, 3761]

原值为764的节点，仅需增加abs(max(8829, 5064) + 764 - max(5929, 7660) + 2725) = 792次，如果采用层级遍历，那么他需要增加 5305 - 764 = 4541次，这样会导致增加不需要增加的次数。

func minIncrements(n int, cost []int) int {
	ans := 0
	for i := n - 2; i > 0; i -= 2 {
		ans += abs(cost[i] - cost[i+1])
		// 叶节点 i 和 i+1 的双亲节点下标为 i/2（整数除法）
		cost[i/2] = cost[i/2] + max(cost[i], cost[i+1])
	}
	return ans
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

func max(i, j int) int {
	if i > j {
		return i
	}
	return j
}

复杂度：

• 时间复杂度：O(N)，其中 N 值为 n
• 空间复杂度：O(1)

执行结果：

• 执行耗时:136 ms,击败了79.17% 的Go用户
• 内存消耗:8.3 MB,击败了12.50% 的Go用户