221. 最大正方形

题目描述：

在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内，找到只包含 ‘1’ 的最大正方形，并返回其面积。

示例 1：

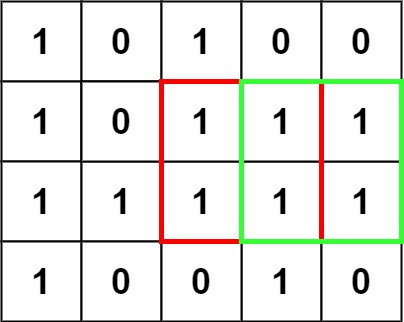
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]
输出：4

示例 2：

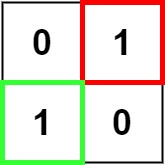
输入：matrix = [["0","1"],["1","0"]]
输出：1

示例 3：

输入：matrix = [["0"]]
输出：0

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 300
• matrix[i][j] 为 ‘0’ 或 ‘1’

---

解题分析及思路：

方法一：动态规划

• 定义状态：dp[i][j] 表示以 matrix[i][j] 为右下角的正方形的最大边长。
• 状态转移方程：dp[i][j] = min(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + 1，即当前位置的最大边长等于左边、上边、左上角三个位置的最大边长的最小值加1。
• 最终结果：maxSide * maxSide

func maximalSquare(matrix [][]byte) int {
	dp := make([][]int, len(matrix))
	maxSide := 0
	for i := 0; i < len(matrix); i++ {
		dp[i] = make([]int, len(matrix[i]))
		for j := 0; j < len(matrix[i]); j++ {
			dp[i][j] = int(matrix[i][j] - '0')
			if dp[i][j] == 1 {
				maxSide = 1
			}
		}
	}

	for i := 1; i < len(matrix); i++ {
		for j := 1; j < len(matrix[i]); j++ {
			if dp[i][j] == 1 {
				dp[i][j] = min(min(dp[i-1][j], dp[i][j-1]), dp[i-1][j-1]) + 1
				if dp[i][j] > maxSide {
					maxSide = dp[i][j]
				}
			}
		}
	}
	return maxSide * maxSide
}

func min(x, y int) int {
	if x < y {
		return x
	}
	return y
}

复杂度：

• 时间复杂度：O(M * N)
• 空间复杂度：O(M * N)

执行结果：

• 执行耗时:5 ms,击败了64.59% 的Go用户
• 内存消耗:6.4 MB,击败了76.56% 的Go用户