3148. 矩阵中的最大得分

题目描述：

给你一个由 正整数 组成、大小为 m x n 的矩阵 grid。你可以从矩阵中的任一单元格移动到另一个位于正下方或正右侧的任意单元格（不必相邻）。从值为 c1 的单元格移动到值为 c2 的单元格的得分为 c2 - c1 。

你可以从 任一 单元格开始，并且必须至少移动一次。

返回你能得到的 最大 总得分。

示例 1：

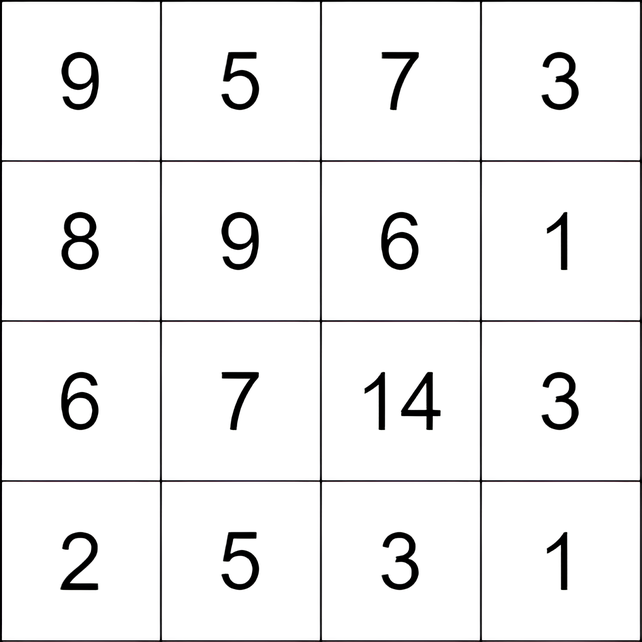
输入： grid = [[9,5,7,3],[8,9,6,1],[6,7,14,3],[2,5,3,1]]
输出： 9
解释： 从单元格 `(0, 1)` 开始，并执行以下移动：
- 从单元格 `(0, 1)` 移动到 `(2, 1)`，得分为 `7 - 5 = 2` 。
- 从单元格 `(2, 1)` 移动到 `(2, 2)`，得分为 `14 - 7 = 7` 。
总得分为 `2 + 7 = 9` 。

示例 2：

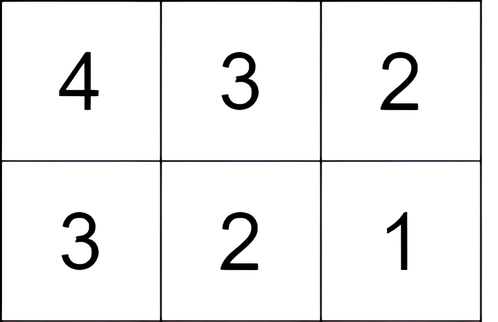
输入： grid = [[4,3,2],[3,2,1]]
输出：-1
解释： 从单元格 `(0, 0)` 开始，执行一次移动：从 `(0, 0)` 到 `(0, 1)` 。得分为 `3 - 4 = -1` 。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• 1 <= grid[i][j] <= 105

---

解题分析及思路：

方法：动态规划

思路：

本题实际是 你需要矩阵中某个单元格移动到该单元格右侧或者下方的任意单元格，可以选择

• 只移动到右侧单元格
• 只移动到下方单元格
• 移动到右侧单元格后再次移动到下方单元格（等同于 移动到下方单元格后再次移动到右侧单元格）

那么，最终移动到单元格(i,j)的元素可以来自(0 ～ i, 0 ～ j)（不包括(i,j)），该区域为单元格(i,j)的左上角。

最终，问题转换为找出位置(i,j)左上角的最小值，即dp[i][j]，最终每个单元格的值 - dp[i][j]，即为得分，取每个结果的最大值为最大得分。

dp[i][j] = min(min(dp[i-1][j], dp[i][j-1]), grid[i][j])

因为需要至少移动一步，所以初始化结果为grid[0][1] - grid[0][0]（即默认从(0,0)移动到(0,1)），后续有更大结果将会更新。

func maxScore(grid [][]int) int {
	m := len(grid)
	n := len(grid[0])
	dp := make([][]int, m)

	for i := range dp {
		dp[i] = make([]int, n)
		for j := range dp[i] {
			dp[i][j] = math.MaxInt32
		}
	}

	ans := grid[0][1] - grid[0][0]
	for i := 0; i < m; i++ {
		for j := 0; j < n; j++ {
			var temp = grid[i][j]
			if i > 0 {
				temp = min(temp, dp[i-1][j])
				ans = max(ans, grid[i][j]-dp[i-1][j])
			}
			if j > 0 {
				temp = min(temp, dp[i][j-1])
				ans = max(ans, grid[i][j]-dp[i][j-1])
			}
			dp[i][j] = temp
		}
	}
	return ans
}

func max(a, b int) int {
	if a > b {
		return a
	}
	return b
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

复杂度：

• 时间复杂度：O(n * m)
• 空间复杂度：O(n * m)

执行结果：

• 执行耗时:115 ms,击败了60.51% 的Go用户
• 内存消耗:8.4 MB,击败了30.77% 的Go用户