2684. 矩阵中移动的最大次数

题目描述：

给你一个下标从 0 开始、大小为 m x n 的矩阵 grid ，矩阵由若干 正 整数组成。

你可以从矩阵第一列中的 任一 单元格出发，按以下方式遍历 grid ：

• 从单元格 (row, col) 可以移动到 (row - 1, col + 1)、(row, col + 1) 和 (row + 1, col + 1) 三个单元格中任一满足值 严格 大于当前单元格的单元格。

返回你在矩阵中能够 移动 的 最大 次数。

示例 1:

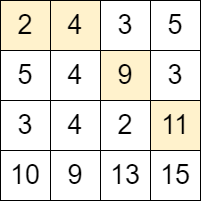
输入：grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]
输出：3
解释：可以从单元格 (0, 0) 开始并且按下面的路径移动：
- (0, 0) -> (0, 1).
- (0, 1) -> (1, 2).
- (1, 2) -> (2, 3).
可以证明这是能够移动的最大次数。

示例 2:

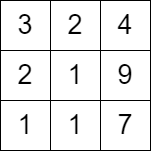
输入：grid = [[3,2,4],[2,1,9],[1,1,7]]
输出：0
解释：从第一列的任一单元格开始都无法移动。

提示：

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 10^5
• 1 <= grid[i][j] <= 10^6

---

解题分析及思路：

从第一列的任一单元格 (i,0) 开始出发。枚举往右上/右/右下三个方向走，每走一步，如果路过的位置的值大于上一步的值，就可以继续走下去。最终返回最大的走的步数。

我们可以把所有可以路过的点放到一个队列里面，每次取队列里的第一个值，判断是否可以继续走下去，如果可以就把可以走的点放到队列里面，以此反复，直到队列为空。

当每次取出的点的列号大于当前的最大步数时，就更新最大步数。

需要注意：

• 为了避免重复走，我们可以把走过的点的值置为0（因为grid二维数组的值都为正数），然后在下一次遍历的时候，如果遇到值为0的点，就直接跳过。
• 需要提前将第一列的点放到队列里面。

func maxMoves(grid [][]int) (result int) {
	rows, cols := len(grid), len(grid[0])
	q := make([][2]int, 0)
	for i := 0; i < rows; i++ {
		q = append(q, [2]int{i, 0})
	}
	for len(q) != 0 {
		num := q[0]
		q = q[1:]
		if grid[num[0]][num[1]] == 0 {
			continue
		}
		q1 := make([][2]int, 0)
		if num[0]-1 >= 0 && num[1]+1 < cols && grid[num[0]-1][num[1]+1] > grid[num[0]][num[1]] {
			q1 = append(q1, [2]int{num[0] - 1, num[1] + 1})
		}
		if num[1]+1 < cols && grid[num[0]][num[1]+1] > grid[num[0]][num[1]] {
			q1 = append(q1, [2]int{num[0], num[1] + 1})
		}
		if num[0]+1 < rows && num[1]+1 < cols && grid[num[0]+1][num[1]+1] > grid[num[0]][num[1]] {
			q1 = append(q1, [2]int{num[0] + 1, num[1] + 1})
		}
		if num[1] > result {
			result = num[1]
		}
		grid[num[0]][num[1]] = 0
		q = append(q, q1...)
	}
	return
}

复杂度：

• 时间复杂度：O(M * N)
• 空间复杂度：O(M * N)

执行结果：

• 执行耗时:138 ms,击败了63.89% 的Go用户
• 内存消耗:8.5 MB,击败了19.44% 的Go用户