662. 二叉树最大宽度

题目描述：

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的 宽度 。

每一层的 宽度 被定义为该层最左和最右的非空节点（即，两个端点）之间的长度。将这个二叉树视作与满二叉树结构相同，两端点间会出现一些延伸到这一层的 null 节点，这些 null 节点也计入长度。

题目数据保证答案将会在  32 位 带符号整数范围内。

测试用例：

示例 1：

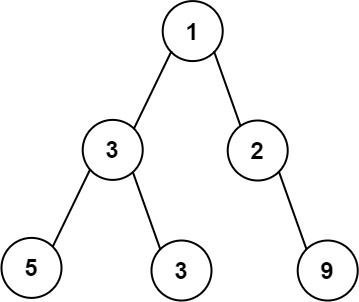
输入：root = [1,3,2,5,3,null,9]
输出：4
解释：最大宽度出现在树的第 3 层，宽度为 4 (5,3,null,9) 。

示例 2：

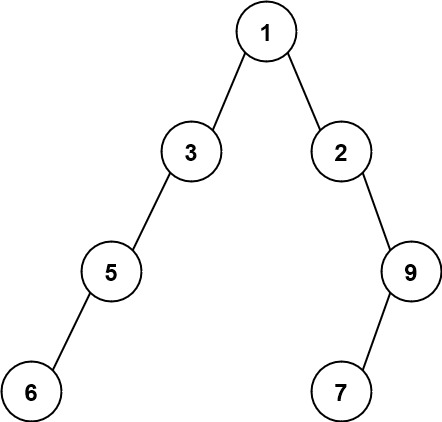
输入：root = [1,3,2,5,null,null,9,6,null,7]
输出：7
解释：最大宽度出现在树的第 4 层，宽度为 7 (6,null,null,null,null,null,7) 。

示例 3：

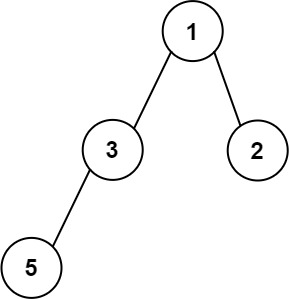
输入：root = [1,3,2,5]
输出：2
解释：最大宽度出现在树的第 2 层，宽度为 2 (3,2) 。

限制及提示：

• 树中节点的数目范围是 [1, 3000]
• -100 <= Node.val <= 100

---

解题分析及思路：

本题采用二叉树 🔗的层级遍历进行解答

在遍历的同时，为每一个节点进行编号，遍历每一层计算当前节点的编号

• 根节点默认编号为1
• 当前节点为父节点（index）的左节点，则当前节点的编号为2*index
• 当前节点为父节点（index）的右节点，则当前节点的编号为2*index+1

遍历每一层，算出这一层的最左边节点的编号left，再遍历得到最右边节点的编号right，那么该层的宽度等于right - left + 1。

遍历整棵树的每一层，计算每一层的宽度，得到最大宽度。

func widthOfBinaryTree(root *TreeNode) (ans int) {

	type Pair struct {
		*TreeNode
		index int
	}

	queue := []Pair{{
		root,
		1,
	}}

	for len(queue) > 0 {
		l := len(queue)
		left := queue[0].index
		right := left
		for i := 0; i < l; i++ {
			if queue[i].Left != nil {
				queue = append(queue, Pair{
					queue[i].Left,
					queue[i].index * 2,
				})
			}
			if queue[i].Right != nil {
				queue = append(queue, Pair{
					queue[i].Right,
					queue[i].index*2 + 1,
				})
			}
			right = queue[i].index
		}
		width := right - left + 1
		if width > ans {
			ans = width
		}
		queue = queue[l:]
	}
	return
}

注意：如果此题最开始未考虑空节点，可能直接遍历每一层的节点数就会有误，其实部分空节点也要计算在内，例如：某一层：1,2,null,null,3，这种宽度为5，而不是3

复杂度：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

执行结果：

• 执行用时：4 ms, 在所有 Go 提交中击败了88.43%的用户
• 内存消耗：4.4 MB, 在所有 Go 提交中击败了60.26%的用户