3071. 在矩阵上写出字母 Y 所需的最少操作次数

题目描述：

给你一个下标从 0 开始、大小为 n x n 的矩阵 grid ，其中 n 为奇数，且 grid[r][c] 的值为 0 、1 或 2 。

如果一个单元格属于以下三条线中的任一一条，我们就认为它是字母 Y 的一部分：

• 从左上角单元格开始到矩阵中心单元格结束的对角线。
• 从右上角单元格开始到矩阵中心单元格结束的对角线。
• 从中心单元格开始到矩阵底部边界结束的垂直线。

当且仅当满足以下全部条件时，可以判定矩阵上写有字母 Y ：

• 属于 Y 的所有单元格的值相等。
• 不属于 Y 的所有单元格的值相等。
• 属于 Y 的单元格的值与不属于Y的单元格的值不同。

每次操作你可以将任意单元格的值改变为 0 、1 或 2 。返回在矩阵上写出字母 Y 所需的 最少 操作次数。

示例 1：

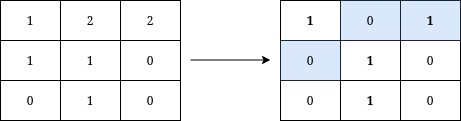
输入：grid = [[1,2,2],[1,1,0],[0,1,0]]
输出：3
解释：将在矩阵上写出字母 Y 需要执行的操作用蓝色高亮显示。操作后，所有属于 Y 的单元格（加粗显示）的值都为 1 ，而不属于 Y 的单元格的值都为 0 。
可以证明，写出 Y 至少需要进行 3 次操作。

示例 2：

输入：grid = [[0,1,0,1,0],[2,1,0,1,2],[2,2,2,0,1],[2,2,2,2,2],[2,1,2,2,2]]
输出：12
解释：将在矩阵上写出字母 Y 需要执行的操作用蓝色高亮显示。操作后，所有属于 Y 的单元格（加粗显示）的值都为 0 ，而不属于 Y 的单元格的值都为 2 。
可以证明，写出 Y 至少需要进行 12 次操作。

提示：

• 3 <= n <= 49
• n == grid.length == grid[i].length
• 0 <= grid[i][j] <= 2
• n 为奇数。

---

解题分析及思路：

思路：

在整个矩阵，需要作出改变的部分一共分为两种：

• 属于 Y 的部分
• 不属于 Y 的部分

我们仅需要考虑这两种部分的改变次数，然后取最小值即可。

而针对两部分的改变次数，其中当确定了属于 Y 的部分的值后，不属于 Y 的部分的值也就确定了。

所以一共有 6 种情况，我们只需要遍历这 6 种情况，然后取最小值即可。

以 Y 最终值为 0，非Y 部分最终值为 1 为例，需要做两件事情：

• 将属于 Y 的部分的值改为 0，统计改变次数
• 将不属于 Y 的部分的值改为 1，统计改变次数

而确认属于 Y 的部分和非 Y 的部分的值可以遍历整个二维数组，分别计算出属于 Y 的部分和非 Y 的部分的值的个数。

一共只有三种类型的值，即0、1、2，所以仅仅分别为属于 Y 的部分和非 Y 的部分建立一个三位的数组保存值即可。

那么，如何确认属于 Y 的部分和非 Y 的部分的值呢？

我们可以通过观察发现，属于 Y 的部分的特点是：

• 从左上角单元格开始到矩阵中心单元格结束的对角线。
• 从右上角单元格开始到矩阵中心单元格结束的对角线。
• 从中心单元格开始到矩阵底部边界结束的垂直线。

所以我们可以通过遍历整个二维数组，然后判断当前位置是否属于 Y 的部分即可。

func minimumOperationsToWriteY(grid [][]int) int {
	var y [3]int
	var notY [3]int
	rowMid := len(grid) / 2
	colMid := len(grid[0]) / 2
	for i := range grid {
		for j := range grid[i] {
			if isY(i, j, rowMid, colMid) {
				y[grid[i][j]]++
			} else {
				notY[grid[i][j]]++
			}
		}
	}
	var res = math.MaxInt
	for i := 0; i < 3; i++ {
		for j := 0; j < 3; j++ {
			if i != j {
				res = min(res, getCount(y, notY, i, j))
			}
		}
	}
	return res
}
func isY(i, j, rowMid, colMid int) bool {
	if i <= rowMid {
		if colMid-i == j-colMid || i == j {
			return true
		}
		return false
	}
	if j == rowMid {
		return true
	}
	return false
}

func getCount(y [3]int, notY [3]int, yValue, notYValue int) int {
	var count int
	for i := 0; i < 3; i++ {
		if i != yValue {
			count += y[i]
		}
		if i != notYValue {
			count += notY[i]
		}
	}
	return count
}

func min(i, j int) int {
	if i < j {
		return i
	}
	return j
}

复杂度：

• 时间复杂度：O(M * N)，其中 M 和 N 分别为 grid 的行数和列数
• 空间复杂度：O(M * N)

执行结果：

• 执行耗时:39 ms,击败了66.90% 的Go用户
• 内存消耗:6.8 MB,击败了81.69% 的Go用户