1319. 连通网络的操作次数

题目描述：

用以太网线缆将 n 台计算机连接成一个网络，计算机的编号从 0 到 n-1。线缆用 connections 表示，其中 connections[i] = [a, b] 连接了计算机 a 和 b。

网络中的任何一台计算机都可以通过网络直接或者间接访问同一个网络中其他任意一台计算机。

给你这个计算机网络的初始布线 connections，你可以拔开任意两台直连计算机之间的线缆，并用它连接一对未直连的计算机。请你计算并返回使所有计算机都连通所需的最少操作次数。如果不可能，则返回 -1 。

示例 1：

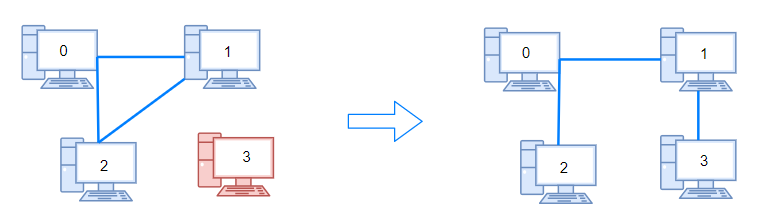
输入：n = 4, connections = [[0,1],[0,2],[1,2]]
输出：1
解释：拔下计算机 1 和 2 之间的线缆，并将它插到计算机 1 和 3 上。

示例 2：

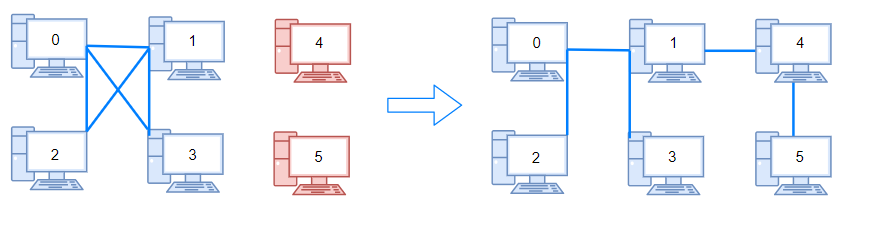
输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2],[1,3]]
输出：2

示例 3：

输入：n = 6, connections = [[0,1],[0,2],[0,3],[1,2]]
输出：-1
解释：线缆数量不足。

示例 4：

输入：n = 5, connections = [[0,1],[0,2],[3,4],[2,3]]
输出：0

提示：

• 1 <= n <= 10^5
• 1 <= connections.length <= min(n*(n-1)/2, 10^5)
• connections[i].length == 2
• 0 <= connections[i][0], connections[i][1] < n
• connections[i][0] != connections[i][1]
• 没有重复的连接。
• 两台计算机不会通过多条线缆连接。

---

解题分析及思路：

方法：并查集

思路：

在n台计算机中，需要至少n-1条线缆才能连接所有计算机，所以可以分为两种情况：

1. 如果线缆数量小于n-1，则所有计算机不能全部连接，返回-1。
2. 如果线缆数量大于等于n-1，则所有计算机都可以全部连接，此时需要求出所有的网络数量，并返回网络数量减去1。

而网络连接问题可以通过并查集来解决，利用并查集，将计算机分为不同的网络，并统计网络数量。

func makeConnected(n int, connections [][]int) int {
	if len(connections) < n-1 {
		return -1
	}
	parent := make([]int, n)
	for i := 0; i < n; i++ {
		parent[i] = i
	}
	var find func(int) int
	find = func(x int) int {
		if parent[x] != x {
			parent[x] = find(parent[x])
		}
		return parent[x]
	}
	var union func(int, int)
	union = func(x, y int) {
		parent[find(x)] = find(y)
	}
	for _, conn := range connections {
		union(conn[0], conn[1])
	}
	var count int
	for i := 0; i < n; i++ {
		if parent[i] == i {
			count++
		}
	}
	return count - 1
}

复杂度：

• 时间复杂度：O(m * 𝛼(n))，其中 m 是数组 connections 的长度，α 是阿克曼函数的反函数。
• 空间复杂度：O(n)

执行结果：

• 执行耗时:49 ms,击败了45.10% 的Go用户
• 内存消耗:9.4 MB,击败了66.67% 的Go用户