2368. 首先条件下可到达节点的数目

题目描述：

现有一棵由 n 个节点组成的无向树，节点编号从 0 到 n - 1 ，共有 n - 1 条边。

给你一个二维整数数组 edges ，长度为 n - 1 ，其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条边。另给你一个整数数组 restricted 表示 受限 节点。

在不访问受限节点的前提下，返回你可以从节点 0 到达的 最多 节点数目。

注意，节点 0 不 会标记为受限节点。

示例 1：

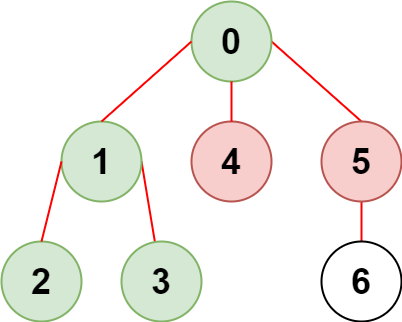
输入：n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]
输出：4
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,1,2,3] 可以从节点 0 到达。

示例 2：

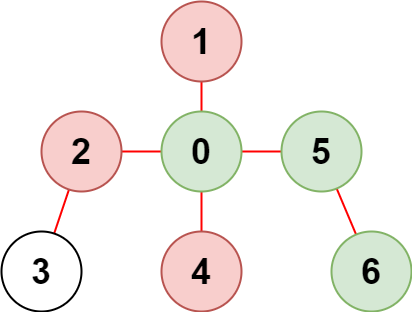
输入：n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]
输出：3
解释：上图所示正是这棵树。
在不访问受限节点的前提下，只有节点 [0,5,6] 可以从节点 0 到达。

提示：

• 2 <= n <= 10^5
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges 表示一棵有效的树
• 1 <= restricted.length < n
• 1 <= restricted[i] < n
• restricted 中的所有值 互不相同

---

解题分析及思路：

思路：

本题可以使用广度优先搜索+哈希表的方式来解决

以 节点 0 为起点，找到与节点 0 相连的节点，存在以下两种情况：

• 该节点是受限节点，不可访问
• 该节点是非受限节点，可访问，采用同种方法，遍历与该节点相连的节点

使用广度优先搜索，找到所有可以到达的节点，然后返回节点数目即可。

那么如何找到受限节点呢？可以使用哈希表的方式，将受限节点存储在哈希表中，然后在遍历的时候，判断是否是受限节点即可。

因为edges为单向的，如果需要保存节点的相连关系， 所以需要将edges转换为双向的，即edges[i][0] = edges[i][1]，edges[i][1] = edges[i][0]。

但是此时，在遍历的时候，会出现重复遍历的情况，所以需要额外增加一个标记表明该节点是已经访问过的，所以需要使用visitedMap来存储已经访问过的节点。

func reachableNodes(n int, edges [][]int, restricted []int) int {
	edgesMap := make(map[int][]int)
	visitedMap := make(map[int]bool)
	for index := range edges {
		edgesMap[edges[index][0]] = append(edgesMap[edges[index][0]], edges[index][1])
		edgesMap[edges[index][1]] = append(edgesMap[edges[index][1]], edges[index][0])
	}
	for index := range restricted {
		visitedMap[restricted[index]] = true
	}
	visitedMap[0] = true
	var count int
	queue := make([]int, 0)
	queue = append(queue, 0)
	for len(queue) != 0 {
		num := queue[0]
		queue = queue[1:]
		for index := range edgesMap[num] {
			if !visitedMap[edgesMap[num][index]] {
				visitedMap[edgesMap[num][index]] = true
				count++
				queue = append(queue, edgesMap[num][index])
			}
		}
	}
	return count + 1
}

复杂度：

• 时间复杂度：O(N)，其中 N 的值为n
• 空间复杂度：O(N)，其中 N 的值为n

执行结果：

• 执行耗时:317 ms,击败了12.67% 的Go用户
• 内存消耗:37.8 MB,击败了30.98% 的Go用户