3128. 直角三角形

题目描述：

给你一个二维 boolean 矩阵 grid 。

请你返回使用 grid 中的 3 个元素可以构建的 直角三角形 数目，且满足 3 个元素值 都 为 1 。

注意：

• 如果 grid 中 3 个元素满足：一个元素与另一个元素在 同一行，同时与第三个元素在 同一列 ，那么这 3 个元素称为一个 直角三角形 。这 3 个元素互相之间不需要相邻。

示例 1：

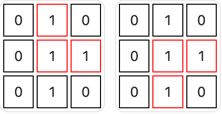
输入： grid = [[0,1,0],[0,1,1],[0,1,0]]

输出： 2

解释：
有 2 个直角三角形。

示例 2：

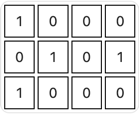
输入： grid = [[1,0,0,0],[0,1,0,1],[1,0,0,0]]

输出： 0

解释：
没有直角三角形。

示例 3：

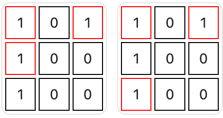
输入： grid = [[1,0,1],[1,0,0],[1,0,0]]

输出： 2

解释：
有两个直角三角形。

提示：

• 1 <= grid.length <= 1000
• 1 <= grid[i].length <= 1000
• 0 <= grid[i][j] <= 1

---

解题分析及思路：

方法：计数

思路：

计算二位矩阵中每一行、每一列中值为1的个数，得到长度为n的数组rowCount和长度为m的数组colCount。

以某一点i,j为直角三角形的直角上的定点，那么此位置能够组成的直角三角形的个数为(rowCount[i] - 1) * (colCount[j] - 1)。

遍历完整个矩阵，将结果累加即可。

func numberOfRightTriangles(grid [][]int) int64 {
	var rowCount = make([]int, len(grid))
	var colCount = make([]int, len(grid[0]))
	for i := range grid {
		for j := range grid[i] {
			rowCount[i] += grid[i][j]
			colCount[j] += grid[i][j]
		}
	}
	var res int64
	for i := range grid {
		for j := range grid[i] {
			if grid[i][j] == 1 {
				res += (int64(rowCount[i]) - 1) * (int64(colCount[j]) - 1)
			}
		}
	}
	return res
}

复杂度：

• 时间复杂度：O(n * m), n为行数，m为列数
• 空间复杂度：O(n)

执行结果：

• 执行耗时:264 ms,击败了54.82% 的Go用户
• 内存消耗:22.7 MB,击败了63.70% 的Go用户