240. 搜索二维矩阵 II

题目描述：

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

• 每行的元素从左到右升序排列。
• 每列的元素从上到下升序排列。

示例1：

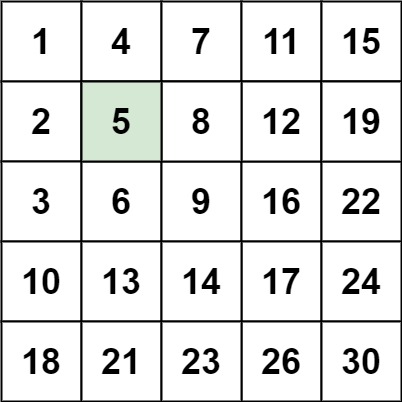
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

示例2：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= n, m <= 300
• -10⁹ <= matrix[i][j] <= 10⁹
• 每行的所有元素从左到右升序排列
• 每列的所有元素从上到下升序排列
• -10⁹ <= target <= 10⁹

---

解题分析及思路：

方法一：二分查找

本题可以从矩阵的左下角或者右上角开始搜索，以右上角为例：

根据矩阵的特性，每行的元素从左到右升序排列，且每列的元素从上到下升序排列。

那么初始 坐标为矩阵右上角坐标

• 当 当前数小于目标值时，横坐标加1
• 当 当前数大于目标值时，纵坐标减1
• 当 当前数等于目标值时，返回为true
• 遍历完成后，即认为不存在目标值在矩阵内，返回false

注意：不能从左上角或者右下角出发，因为根据当前数周围值的情况，无法判断大小，可能出现同时小于/大于的情况

func searchMatrix(matrix [][]int, target int) bool {
	if matrix[0][0] > target || matrix[len(matrix)-1][len(matrix[0])-1] < target {
		return false
	}
	rows, cols := len(matrix), len(matrix[0])
	row, col := 0, cols-1
	for row < rows && col >= 0 {
		if matrix[row][col] == target {
			return true
		}
		for row < rows && col >= 0 && matrix[row][col] < target {
			row++
		}
		for row < rows && col >= 0 && matrix[row][col] > target {
			col--
		}
	}
	return false
}

复杂度：

• 时间复杂度：O(M + N)
• 空间复杂度：O(1)

执行结果：

• 执行耗时:16 ms,击败了62.30% 的Go用户
• 内存消耗:6.2 MB,击败了98.97% 的Go用户