1260. 二维网格迁移

题目描述：

给你一个 m 行 n 列的二维网格 grid 和一个整数 k。你需要将 grid 迁移 k 次。

每次「迁移」操作将会引发下述活动

位于 grid[i][j] 的元素将会移动到 grid[i][j + 1]。

位于 grid[i][n - 1] 的元素将会移动到 grid[i + 1][0]。

位于 grid[m - 1][n - 1] 的元素将会移动到 grid[0][0]。

请你返回 k 次迁移操作后最终得到的 二维网格。

测试用例：

示例 1:

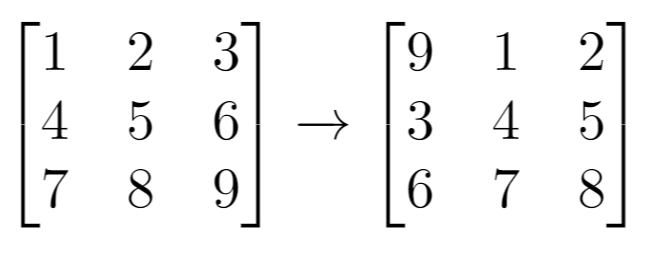
输入：grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
输出：[[9,1,2],[3,4,5],[6,7,8]]

示例 2：

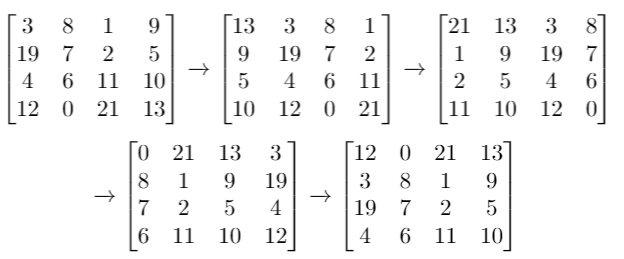
输入：grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4

输出：[[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

限制及提示：

• m == grid.length
• n == grid[i].length
• 1 <= m <= 50
• 1 <= n <= 50
• -1000 <= grid[i][j] <= 1000
• 0 <= k <= 100

---

解题分析及思路：

本题中迁移的意思就是每个坐标的数往后移动一位，如果已经处于最后一列，则移到下一行第一列。

所以迁移k次，就是将数往后移动k位。

对于行列分别为rows, cols的二维数组，将其进行扁平化成一维数组，那么其元素（i,j）在进行k此移动后，元素（i,j）在一维数组中所对应的下标为 index = (i*cols + j + k) % (rows * cols).

再将一维数组填回新的二维数组，则index所对应的二维数组下标为(index/cols,index%cols)

for i, row := range grid {
    for j, v := range row {
        index := (i*cols + j + k) % (rows * cols)
        ans[index/cols][index%cols] = v
    }
}

复杂度：

• 时间复杂度：O(m * n)
• 空间复杂度：O(1)

执行结果：

• 执行用时： 8 ms , 在所有 Go 提交中击败了 100.00% 的用户
• 内存消耗： 6.8 MB , 在所有 Go 提交中击败了 85.37% 的用户