130. 被围绕的区域

题目描述：

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' 组成， 捕获 所有 被围绕的区域：

• 连接： 一个单元格与水平或垂直方向上相邻的单元格连接。
• 区域：连接所有 'O' 的单元格来形成一个区域。
• 围绕： 如果您可以用 'X' 单元格 连接这个区域，并且区域中没有任何单元格位于 board 边缘，则该区域被 'X' 单元格围绕。

通过 原地 将输入矩阵中的所有 'O' 替换为 'X' 来 捕获被围绕的区域。你不需要返回任何值。

示例 1：

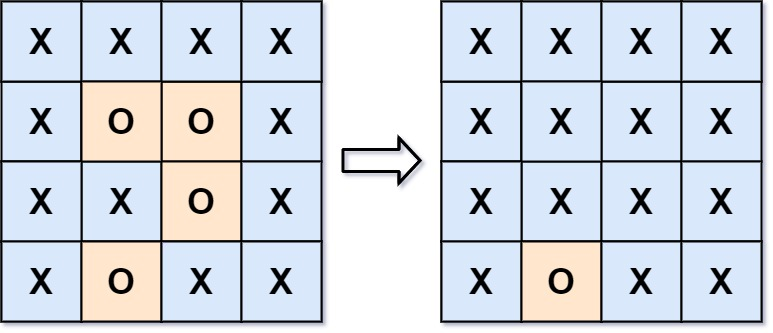
输入： board = '['["X","X","X","X"'],'["X","O","O","X"'],'["X","X","O","X"'],'["X","O","X","X"']']

输出：'['["X","X","X","X"'],'["X","X","X","X"'],'["X","X","X","X"'],'["X","O","X","X"']']

解释：


在上图中，底部的区域没有被捕获，因为它在 board 的边缘并且不能被围绕。

示例 2：

输入： board = '['["X"']']

输出：'['["X"']']

提示：

• m == board.length
• n == board[i].length
• 1 <= m, n <= 200
• board[i][j] 为 'X' 或 'O'

---

解题分析及思路：

方法：深度优先搜索

思路：

本题的关键是要明确：“被围绕的区域” 本质是 “不与边界连通的 ‘O’ 区域”。

• 若一个 ‘O’ 位于边界，或能通过上下左右路径连接到边界的 ‘O’，则它一定不会被围绕（因为存在通向边界的 “出口”）。
• 反之，若一个 ‘O’ 既不在边界，又无法连接到任何边界的 ‘O’，则它必然被 ‘X’ 完全包围，需要被转换。

因此，算法的核心思路可概括为：

• 标记 “安全区域”：先找到所有与边界 ‘O’ 连通的 ‘O’，将它们标记为 “安全”（避免被转换）。
• 清理 “非安全区域”：将未被标记的 ‘O’（即被围绕的区域）转换为 ‘X’，同时还原 “安全区域” 的标记。

步骤 1：标记与边界连通的 ‘O’（安全区域）

• 遍历边界：矩阵的边界包括第一行、最后一行、第一列、最后一列。对这些位置上的 ‘O’ 进行深度优先搜索（DFS）。
• DFS 扩散标记：从边界的 ‘O’ 出发，递归遍历其上下左右四个方向的相邻单元格。遇到 ‘O’ 就将其标记为临时字符（如 ‘U’，表示 “未被围绕”），避免重复处理。

为什么要标记？

如果直接在遍历过程中修改为 ‘O’，会导致后续无法区分 “原始 ‘O’” 和 “已处理的 ‘O’”，可能引发无限递归或漏处理。临时标记 ‘U’ 是一种安全的中间状态。

步骤 2：更新矩阵（区分安全与非安全区域）

• 再次遍历整个矩阵：
  • 若单元格为 ‘O’：说明它未被标记为安全区域（不与边界连通），是被围绕的，需转换为 ‘X’。
  • 若单元格为 ‘U’：说明它是安全区域（与边界连通），需还原为 ‘O’。

func solve(board [][]byte) {
	var dfs func(i, j int)
	dfs = func(i, j int) {
		if i < 0 || j < 0 || i >= len(board) || j >= len(board[i]) || board[i][j] != 'O' {
			return
		}
		board[i][j] = 'U'
		dfs(i-1, j)
		dfs(i+1, j)
		dfs(i, j-1)
		dfs(i, j+1)
	}
	for i := range board {
		for j := range board[i] {
			if (i == 0 || i == len(board)-1 || j == 0 || j == len(board[i])-1) && board[i][j] == 'O' {
				dfs(i, j)
			}
		}
	}
	for i := range board {
		for j := range board[i] {
			if board[i][j] == 'O' {
				board[i][j] = 'X'
			}
			if board[i][j] == 'U' {
				board[i][j] = 'O'
			}
		}
	}
	return
}

复杂度：

• 时间复杂度：O(m*n)
• 空间复杂度：O(m*n)

执行结果：

• 执行耗时:0 ms,击败了100.00% 的Go用户
• 内存消耗:7.9 MB,击败了94.79% 的Go用户