42. 接雨水
题目描述:
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。

示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
提示:
- n == height.length
- 1 <= n <= 2 * 10^4
- 0 <= height[i] <= 10^5
解题分析及思路:
对于下标 i,下雨后水能到达的最大高度等于下标 i 两边的最大高度的最小值,下标 i 处能接的雨水量等于下标 i 处的水能到达的最大高度减去 height[i]。
首先,我们可以使用动态规划的思想,通过一次正向遍历,预处理得到每个位置左侧和右侧的最大高度。
创建两个数组 maxL 和 maxR,其中 maxL[i] 表示下标 i 及其左边的位置中,height 的最大高度,maxR[i] 表示下标 i 及其右边的位置中,height 的最大高度。
最后,下标i处能够接到的水为minFunc(maxL[i], maxR[i]) - height[i],将所有的求和即为最终答案。
那么对应动态规划解法:
-
定义状态: 在这个问题中,我们可以定义状态为每个位置的左侧最大高度和右侧最大高度。我们使用两个数组 maxL 和 maxR 分别表示每个位置左侧和右侧的最大高度。
-
找到状态转移方程: 通过一次遍历,我们可以计算得到每个位置的左侧最大高度和右侧最大高度。状态转移方程为:
maxL[i] = max(height[i], maxL[i-1])
maxR[l-1-i] = max(height[l-1-i], maxR[l-i])
-
初始化: 初始化数组 maxL 和 maxR 中的第一个元素为对应位置的高度值。
-
递推求解: 通过一次遍历,更新每个位置的左侧最大高度和右侧最大高度。
-
计算最终结果: 通过再次遍历,计算每个位置上的雨水量,总和即为结果。
func trap(height []int) int {
var maxFunc = func(i, j int) int {
if i > j {
return i
}
return j
}
var minFunc = func(i, j int) int {
if i > j {
return j
}
return i
}
var l = len(height)
var maxL = make([]int, l)
var maxR = make([]int, l)
for i := 0; i < l; i++ {
maxL[i] = height[i]
maxR[l-1-i] = height[l-1-i]
if i != 0 {
maxL[i] = maxFunc(maxL[i], maxL[i-1])
maxR[l-1-i] = maxFunc(maxR[l-1-i], maxR[l-i])
}
}
var total int
for i := 0; i < l; i++ {
total += minFunc(maxL[i], maxR[i]) - height[i]
}
return total
}
整体的动态规划思路是通过两次遍历,分别计算每个位置的左侧和右侧最大高度,然后通过再次遍历计算每个位置上的雨水量,最终得到总的雨水量。
复杂度:
- 时间复杂度:O(N),其中 n 为输入数组 height 的长度。
- 空间复杂度:O(N),其中 n 为输入数组 height 的长度。
执行结果:
- 执行耗时:8 ms,击败了89.64% 的Go用户
- 内存消耗:5.9 MB,击败了24.68% 的Go用户
Tags :
通过次数 1.4M 提交次数 2.2M 通过率 65.5%
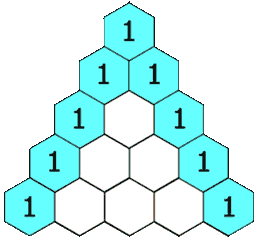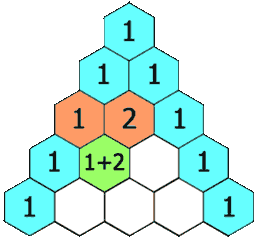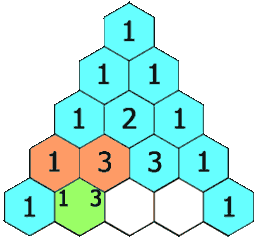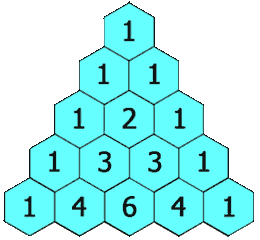 示例 1:
```
输入: numRows = 5
输出: [[1],[1,1],[1,
示例 1:
```
输入: numRows = 5
输出: [[1],[1,1],[1,