118. 杨辉三角

题目描述：

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

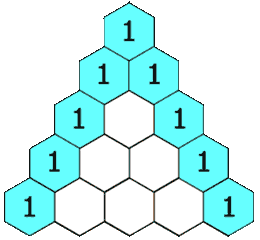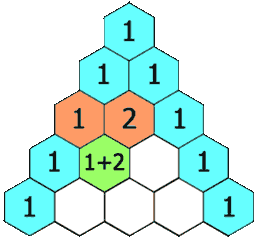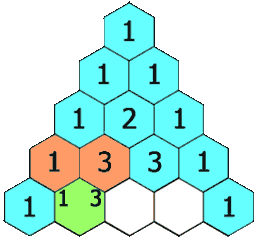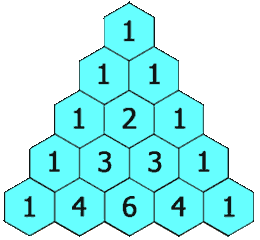示例 1：

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2：

输入: numRows = 1
输出: [[1]]

提示：

• 1 <= numRows <= 30

---

解题分析及思路：

本题可以采取动态规划的方法，生成杨辉三角。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

所以得出状态转移方程：

dp[i][j] = dp[i-1][j-1] + dp[i-1][j]

根据状态转移方程，结合边界条件，可以得出：

• 当 j=0 或 j=i 时，第 j 个数为 1。
• 当 j>0 且 j<i 时，第 j 个数为第 i-1 行的第 j-1 个数和第 j 个数之和。

func generate(numRows int) (result [][]int) {
	for i := 0; i < numRows; i++ {
		var row []int
		for j := 0; j <= i; j++ {
			if j == 0 || j == i {
				row = append(row, 1)
			} else {
				row = append(row, result[i-1][j]+result[i-1][j-1])
			}
		}
		result = append(result, row)
	}
	return
}

复杂度：

• 时间复杂度：O(N)，其中 N 是 numRows 的值。
• 空间复杂度：O(1)。

执行结果：

• 执行耗时:0 ms,击败了100.00% 的Go用户
• 内存消耗:2.3 MB,击败了22.18% 的Go用户