108. 将有序数组转换为二叉搜索树
题目描述:
给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 高度平衡 二叉搜索树。
高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。
示例 1:

输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案

示例 2:
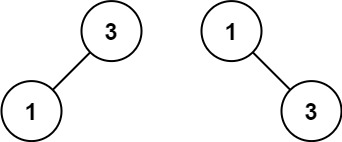
输入:nums = [1,3]
输出:[3,1]
解释:[1,null,3] 和 [3,1] 都是高度平衡二叉搜索树。
提示:
- 1 <= nums.length <= 10^4
- -10^4 <= nums[i] <= 10^4
- nums 按 严格递增 顺序排列
解题分析及思路:
这道题考察的是二叉树的遍历,不熟悉二叉树的遍历可以查看二叉树。
这道题有关二叉搜索树
方法一:递归
由于二叉搜索树的中序遍历本身就是一个递增的序列,所以可以通过中序遍历的方式来解决。
对于有序数组,可以选择中间位置作为根节点,然后递归的构建左子树和右子树。
- 选择中间位置左边的数字作为左子树
- 选择中间位置右边的数字作为右子树
func sortedArrayToBST(nums []int) *TreeNode {
l := len(nums)
if l == 0 {
return nil
}
index := l / 2
return &TreeNode{
Val: nums[index],
Left: sortedArrayToBST(nums[:index]),
Right: sortedArrayToBST(nums[index+1:]),
}
}
复杂度:
- 时间复杂度:O(N),其中 N 是树中的节点个数
- 空间复杂度:O(1)
执行结果:
- 执行耗时:2 ms,击败了45.38% 的Go用户
- 内存消耗:3.3 MB,击败了88.28% 的Go用户

 示例 1:
```
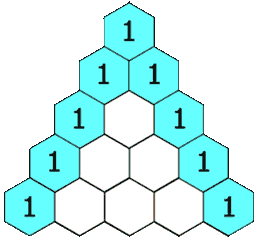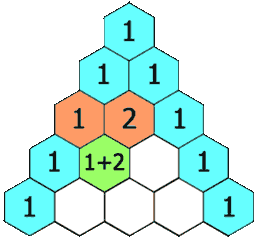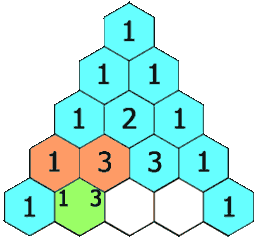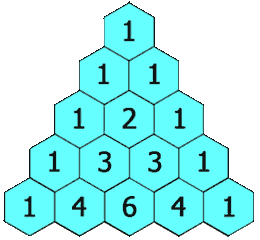
输入: numRows = 5
输出: [[1],[1,1],[1,
示例 1:
```
输入: numRows = 5
输出: [[1],[1,1],[1,