二叉树
二叉树是我们常见的数据结构之一,在学习二叉树之前我们需要知道什么是树,什么是二叉树,本篇主要讲述了二叉树,以及二叉树的遍历。
这里只做算法的相关记录,更多与二叉树有关的基础知识可以访问:还不会二叉树?一篇搞定二叉树 🔗
遍历二叉树主要有四种方法:①:前序遍历 ②:中序遍历 ③:后序遍历 ④:层序遍历
需要事先说明的就是前三种遍历,就是根节点的访问顺序不同,但是访问左右节点的顺序仍然是先访问左结点,再访问右结点。
递归遍历
①:前序遍历
1、访问根节点;
2、访问当前节点的左子树;
3、访问当前节点的右子树;
就是先从根节点出发,先访问根节点,然后访问根结点的左子树,若该左子树的根节点上存在左子树,则访问其左子树,否则,访问其右子树,依次类推。
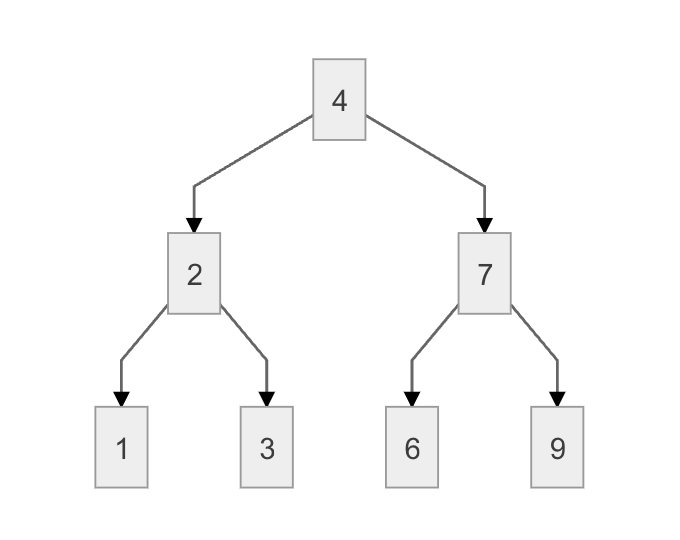
以上图为例,
- 先找到根节点,读取4,
- 该结点还有左子树,访问其左子树的根节点,读取2,
- 结点2,还有左子树,读取1,
- 结点1没有左子树也没有右子树,返回上一层,访问结点2的右子树,读取3,
- 这时候应该访问3的左右子树,但是没有,返回上一层,此时结点2的左右子树都已经读取完,返回上一层,读取结点4的右子树,读取7,
- 访问结点7的左子树,读取6,
- 结点6没有左右子树,返回上一层,访问结点7的右子树,读取9,
- 结点9没有左右子树,这时候该二叉树已经遍历完成。
所以访问到的顺序为:4 2 1 3 7 6 9
②:中序遍历
1、访问当前节点的左子树;
2、访问根节点;
3、访问当前节点的右子树;
遍历思想与前序差不多,只不过将读取根节点放在读取左结点之后、右结点之前
③:后序遍历
1、访问当前节点的左子树;
2、访问当前节点的右子树;
3、访问根节点;
遍历思想与前序差不多,只不过将读取根节点放在读取左结点之后、右结点之后
代码实现:
package tree
// 前序遍历(递归)
func preTraversal(root *TreeNode) {
if root == nil {
return
}
fmt.Print(root.Val, "\t")
preTraversal(root.Left)
preTraversal(root.Right)
}
// 中序遍历(递归)
func miTraversal(root *TreeNode) {
if root == nil {
return
}
miTraversal(root.Left)
fmt.Print(root.Val, "\t")
miTraversal(root.Right)
}
// 后序遍历(递归)
func nextTraversal(root *TreeNode) {
if root == nil {
return
}
nextTraversal(root.Left)
nextTraversal(root.Right)
fmt.Print(root.Val, "\t")
}
以上是关于二叉树的递归实现方法
非递归遍历
① :前序遍历 ② :中序遍历 ③:后续遍历
实现二叉树的非递归实现的核心就是使用栈,而Go语言中没有栈的基本数据结构实现,就需要我们使用切片来实现栈。
- 定义栈:使用
stack := make([]*TreeNode, 0)定义一个栈, - 入栈:切片追加:
stack = append(stack, root) - 出栈:取最后一个结果,然后将切片前len -1 个数拷贝到原有切片中:
root = stack[len(stack)-1];stack = stack[:len(stack)-1]
④:层序遍历
按照二叉树的层级结构从左至右依次遍历结点 算法思路:定义一个队列,从树的根结点开始,依次将其左孩子和右孩子入队。而后每次队列中一个结点出队,都将其左孩子和右孩子入队,直到树中所有结点都出队,出队结点的先后顺序就是层次遍历的最终结果。

- 根节点4入队,
- 根节点4出队,访问结点4的左右结点(2,7),依次入队,
- 结点2出队,访问结点2的左右结点(1,3),依次入队,
- 结点1出队,无子结点,无需入队,
- 结点3出队,无子结点,无需入队,
- 结点6出队,无子结点,无需入队,
- 结点9出队,无子结点,无需入队,
- 队列为空,遍历完成。
最后访问顺序为:4 2 7 1 3 6 9
package tree
// 前序遍历
func preTraversal1(root *TreeNode) {
if root == nil {
return
}
stack := make([]*TreeNode, 0)
for root != nil || len(stack) != 0 {
for root != nil {
stack = append(stack, root)
fmt.Print(root.Val, "\t")
root = root.Left
}
root = stack[len(stack)-1]
stack = stack[:len(stack)-1]
root = root.Right
}
}
// 中序遍历
func miTraversal1(root *TreeNode) {
if root == nil {
return
}
stack := make([]*TreeNode, 0)
for root != nil || len(stack) != 0 {
for root != nil {
stack = append(stack, root)
root = root.Left
}
root = stack[len(stack)-1]
stack = stack[:len(stack)-1]
fmt.Print(root.Val, "\t")
root = root.Right
}
}
// 后序遍历
func nextTraversal1(root *TreeNode) {
if root == nil {
return
}
stack := make([]*TreeNode, 0)
var lastVisit *TreeNode
for root != nil || len(stack) != 0 {
for root != nil {
stack = append(stack, root)
root = root.Left
}
node := stack[len(stack)-1]
if node.Right == nil || node.Right == lastVisit {
stack = stack[:len(stack)-1] // pop
fmt.Print(node.Val, "\t")
// 标记当前这个节点已经弹出过
lastVisit = node
} else {
root = node.Right
}
}
}
// 层级遍历
func levelTraversal(root *TreeNode) {
if root == nil {
return
}
queue := make([]*TreeNode, 0)
for root != nil || len(queue) != 0 {
fmt.Print(root.Val, "\t")
if root.Left != nil {
queue = append(queue, root.Left)
}
if root.Right != nil {
queue = append(queue, root.Right)
}
if len(queue) == 0 {
root = nil
} else {
root = queue[0]
queue = queue[1:]
}
}
}
二叉树应用
后序遍历
层级遍历
二叉树构造
此方法或数据结构有更多算法实例,请点击二叉树 查看更多