889. 根据前序与后序遍历构造二叉树

题目描述：

给定两个整数数组，preorder 和 postorder ，其中 preorder 是一个具有 无重复 值的二叉树的前序遍历，postorder 是同一棵树的后序遍历，重构并返回二叉树。

如果存在多个答案，您可以返回其中 任何 一个。

示例 1：

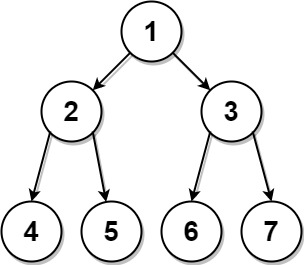
输入：preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1] 
输出：[1,2,3,4,5,6,7]

示例 2：

输入: preorder = [1], postorder = [1]
输出: [1]

提示：

• 1 <= preorder.length <= 30
• 1 <= preorder[i] <= preorder.length
• preorder 中所有值都 不同
• postorder.length == preorder.length
• 1 <= postorder[i] <= postorder.length
• postorder 中所有值都 不同
• 保证 preorder 和 postorder 是同一棵二叉树的前序遍历和后序遍历

---

解题分析及思路：

这道题考察的是二叉树的遍历，不熟悉二叉树的遍历可以查看二叉树。

题目给出的是前序遍历和后序遍历后的结果，由此重新生成原有的二叉树。

将一棵二叉树分别进行前序遍历和后序遍历：

• 针对前序遍历后的结果，可以分析出结果的构成为[ 根节点, [左子树的前序遍历结果], [右子树的前序遍历结果] ]
• 针对后序遍历后的结果，可以分析出结果的构成为[ [左子树的前序遍历结果], [右子树的前序遍历结果], 根节点 ]

而我们仅仅只需要根据前序遍历的第一个值，也就是根节点的值，即可定位到中序遍历根节点的位置。但是，由于后序遍历的结果中，根节点的位置是在最后一个，这样无法区分左右子树的边界。

因此，会有以下两种情形：

• 原二叉树的根节点的左子树不为空，那么前序遍历根节点后一个元素对应左子树的根节点；
• 原二叉树的根节点的左子树为空，那么前序遍历根节点后一个元素对应右子树的根节点。

针对以上两种情况：

• 如果是前者，那么我们可以根据前序遍历的根节点的下一个元素，定位到后序遍历的根节点的位置，从而可以将所有的数据划分为根节点的左右子树。
• 如果是后者，左子树为空，所有的数据划分为根节点的右子树，将右子树移动到左子树的位置，原子树和右子树的前序遍历和后序遍历的结果一致，均满足题意（如果存在多个答案，您可以返回其中 任何 一个）。

所以，无论以上那种情况，我们都可以将前序遍历中的根节点的下一个元素充当左子树的根节点，然后根据后序遍历中左子树的根节点的位置，可以将所有的数据划分为根节点的左右子树。

最后采取同样的方式（递归解决）分别定位左右子树的值及其子树。

其中，定位到根节点的左子树的根节点在后序遍历的下标为left:

• 左子树的的前序遍历集合为preorder[1:left+1]，左子树的后序遍历集合为postorder[:left]
• 右子树的的前序遍历集合为preorder[left+1:]，右子树的后序遍历集合为postorder[left:len(postorder)-1]

func constructFromPrePost(preorder []int, postorder []int) *TreeNode {
	if len(preorder) == 0 {
		return nil
	}
	root := &TreeNode{Val: preorder[0]}
	if len(preorder) == 1 {
		return root
	}
	left := 0
	for i, v := range postorder {
		if v == preorder[1] {
			left = i + 1
		}
	}
	root.Left = constructFromPrePost(preorder[1:left+1], postorder[:left])
	root.Right = constructFromPrePost(preorder[left+1:], postorder[left:len(postorder)-1])
	return root
}

复杂度：

• 时间复杂度：O(N)，其中 N 是树中的节点个数.
• 空间复杂度：O(1)，只使用常数额外空间。

执行结果：

• 执行耗时:4 ms,击败了46.06% 的Go用户
• 内存消耗:2.8 MB,击败了98.18% 的Go用户