62. 不同路径

题目描述：

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

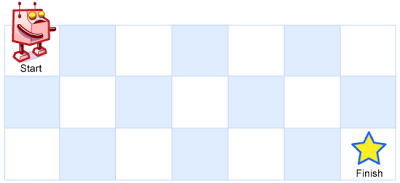
示例 1：

输入：m = 3, n = 7 
输出：28 

示例 2：

输入：m = 3, n = 2 
输出：3 
解释： 从左上角开始，总共有 3 条路径可以到达右下角。 
  1. 向右 -> 向下 -> 向下 
  2. 向下 -> 向下 -> 向右 
  3. 向下 -> 向右 -> 向下

示例 3：

输入：m = 7, n = 3 
输出：28

示例 4：

输入：m = 3, n = 3 
输出：6

提示：

• 1 <= m, n <= 100
• 题目数据保证答案小于等于 2 * 109

---

解题分析及思路：

由于机器人只能向下或者向右移动，所以对于机器人所在位置(i,j),那么他的上一步有两种可能：

• 如果向下走一步，那么会从 (i−1,j) 走过来；
• 如果向右走一步，那么会从(i,j−1)走过来。

所以对应的状态转移方程为：f(i,j)=f(i−1,j)+f(i,j−1)

所以我们可以定义一个长宽为m*n的二维数组，表示机器人能够走到(i,j)的不同的路径条数。

最后，最终的答案即为 f(m−1,n−1)。

那么对应动态规划解法：

1. 定义状态： 在这个问题中，状态可以定义为到达每个位置时的不同路径数量。我们使用二维数组 dp 表示状态，其中 dp[i][j] 表示到达网格位置 (i, j) 时的不同路径数量。

2. 找到状态转移方程： 机器人每次只能向下或者向右移动一步，因此到达当前位置 (i, j) 的不同路径数量等于到达上方位置 (i-1, j) 和到达左方位置 (i, j-1) 的路径数量之和。状态转移方程可以表示为：

dp[i][j] = dp[i-1][j] + dp[i][j-1]

3. 初始化： 在初始化阶段，我们遍历第一行和第一列，将每个位置的路径数量初始化为1，因为机器人只能向下或向右移动，所以沿着第一行和第一列的路径数量都只有一种。

4. 递推求解： 通过嵌套循环遍历整个二维数组，根据状态转移方程计算每个位置的不同路径数量。

5. 计算最终结果： 最终结果即为到达右下角位置 (m-1, n-1) 时的不同路径数量。

func uniquePaths(m int, n int) int {
	var dp = make([][]int, m)
	// init dp
	for i := 0; i < m; i++ {
		dp[i] = make([]int, n)
	}
	for i := 0; i < m; i++ {
		dp[i][0] = 1
	}
	for i := 0; i < n; i++ {
		dp[0][i] = 1
	}
	for i := 1; i < m; i++ {
		for j := 1; j < n; j++ {
			dp[i][j] = dp[i-1][j] + dp[i][j-1]
		}
	}
	return dp[m-1][n-1]
}

复杂度：

• 时间复杂度：O(M*N)，其中 M 为 m 的值，N 为 n 的值。
• 空间复杂度：O(M*N)，其中 M 为 m 的值，N 为 n 的值。

执行结果：

• 执行耗时:0 ms,击败了100.00% 的Go用户
• 内存消耗:2 MB,击败了61.56% 的Go用户