2476. 二叉搜索树最近节点查询

题目描述：

给你一个 二叉搜索树 的根节点 root ，和一个由正整数组成、长度为 n 的数组 queries 。

请你找出一个长度为 n 的 二维 答案数组 answer ，其中 answer[i] = [mini, maxi] ：

• mini 是树中小于等于 queries[i] 的 最大值 。如果不存在这样的值，则使用 -1 代替。
• maxi 是树中大于等于 queries[i] 的 最小值 。如果不存在这样的值，则使用 -1 代替。 返回数组 answer 。

示例 1：

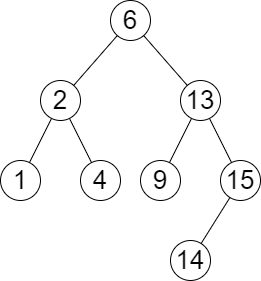
输入：root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16]
输出：[[2,2],[4,6],[15,-1]]
解释：按下面的描述找出并返回查询的答案：
- 树中小于等于 2 的最大值是 2 ，且大于等于 2 的最小值也是 2 。所以第一个查询的答案是 [2,2] 。
- 树中小于等于 5 的最大值是 4 ，且大于等于 5 的最小值是 6 。所以第二个查询的答案是 [4,6] 。
- 树中小于等于 16 的最大值是 15 ，且大于等于 16 的最小值不存在。所以第三个查询的答案是 [15,-1] 。

示例 2：

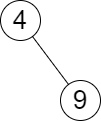
输入：root = [4,null,9], queries = [3]
输出：[[-1,4]]
解释：树中不存在小于等于 3 的最大值，且大于等于 3 的最小值是 4 。所以查询的答案是 [-1,4] 。

提示：

• 树中节点的数目在范围 [2, 10^5] 内
• 1 <= Node.val <= 10^6
• n == queries.length
• 1 <= n <= 10^5

---

解题分析及思路：

这道题考察的是二叉树的遍历，不熟悉二叉树的遍历可以查看二叉树。

这道题有关二叉搜索树

方法：深度优先搜索+二分查找

由于是二叉搜索树，所以可以利用二叉搜索树的性质来解决这个问题。

首先，可以通过二叉搜索树的中序遍历来得到一个递增的序列，然后对于每一个查询，可以通过二分查找来得到最大值和最小值。

针对在序列中找到某个值的下标：

• 如果索引 searchIndex 合法存在，则此时大于等于 val 的最小元素即为 arr[searchIndex]，否则则为 −1，如果此时 arr[searchIndex]=val，则小于等于 val 的最大元素也为 arr[searchIndex]。
• 如果索引 searchIndex 大于 0，则此时小于等于 val 的最大元素即为 arr[searchIndex−1]，否则则为 −1。

注意：如果直接在二叉搜索树上进行查找，虽然说复杂度是一样的，但是可能会有超时的问题。

func closestNodes(root *TreeNode, queries []int) [][]int {
	var nums []int
	var dfs func(root *TreeNode)
	dfs = func(root *TreeNode) {
		if root == nil {
			return
		}
		dfs(root.Left)
		nums = append(nums, root.Val)
		dfs(root.Right)
	}
	dfs(root)
	midSearch := func(x int) int {
		left := 0
		right := len(nums)
		for left < right {
			mid := left + (right-left)/2
			if nums[mid] >= x {
				right = mid
			} else {
				left = mid + 1
			}
		}
		return left
	}
	result := make([][]int, len(queries))
	for index := range queries {
		min, max := -1, -1
		searchIndex := midSearch(queries[index])
		if searchIndex < len(nums) {
			max = nums[searchIndex]
			if nums[searchIndex] == queries[index] {
				min = nums[searchIndex]
				result[index] = []int{min, max}
				continue
			}
		}
		if searchIndex != 0 {
			min = nums[searchIndex-1]
		}
		result[index] = []int{min, max}
	}
	return result
}

复杂度：

• 时间复杂度：O(N + Q *logN)，其中 N 是树中的节点个数，Q 表示给定的查询数组的长度。
• 空间复杂度：O(N)，其中 N 是树中的节点个数

执行结果：

• 执行耗时:346 ms,击败了34.38% 的Go用户
• 内存消耗:41.6 MB,击败了81.25% 的Go用户