3200. 三角形的最大高度

题目描述：

给你两个整数 red 和 blue，分别表示红色球和蓝色球的数量。你需要使用这些球来组成一个三角形，满足第 1 行有 1 个球，第 2 行有 2 个球，第 3 行有 3 个球，依此类推。

每一行的球必须是 相同 颜色，且相邻行的颜色必须 不同。

返回可以实现的三角形的 最大 高度。

示例 1：

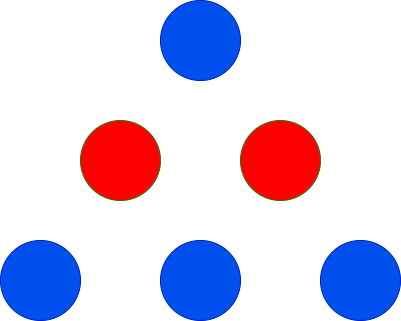
输入： red = 2, blue = 4

输出： 3

解释：


上图显示了唯一可能的排列方式。

示例 2：

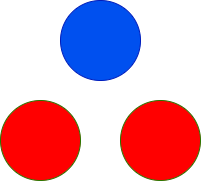
输入： red = 2, blue = 1

输出： 2

解释：

上图显示了唯一可能的排列方式。

示例 3：

输入： red = 1, blue = 1

输出： 1

示例 4：

输入： red = 10, blue = 1

输出： 2

解释：

上图显示了唯一可能的排列方式。

提示：

• 1 <= red, blue <= 100

---

解题分析及思路：

方法：数学

思路：

可以看出来，对于不同的球，摆放的可能有两种情况：

1. 摆放在第一行，第三行，第五行，第七行，……；
2. 摆放在第二行，第四行，第六行，……；

那么，摆放球的个数形成一个等差数列，那么，求解等差数列中，最小的项数，就是最大的三角形高度。

等差数列有几个关键值：

• 公差：b
• 和：Sn
• 起始值：a
• 项数：n

其求和公式为：Sn = (n / 2) * (2a + (n - 1) * b)

由于公差固定为2，那么化简后，可以得到：

Sn = (n / 2) * (2a + (n - 1) * 2)
=>
n^2 * b + n * (2a - b) - 2 * Sn = 0
=>
n^2 + n * (a - 1) - Sn = 0

那么对于一元二次方程，项数n的解为： n = (-B ± sqrt(B^2 - 4AC)) / 2A

由于 (-B - sqrt(B^2 - 4AC)) / 2A 为负数，所以，我们取正数解(-B + sqrt(B^2 - 4AC)) / 2A

利用findNumberOfTerms方法得到蓝球和红球放在单数层和双数层的行数：

• 蓝球：blueLayer1（单数层）, blueLayer2（双数层）
• 红球：redLayer1（单数层）, redLayer2（双数层）

那么，最大的三角形高度为：min(blueLayer1*2-1, redLayer2*2)和 min(blueLayer2*2, redLayer1*2-1) 中的较大值，并且要加一。

func maxHeightOfTriangle(red int, blue int) int {
	blueLayer1, blueLayer2 := findNumberOfTerms(1, blue), findNumberOfTerms(2, blue)
	redLayer1, redLayer2 := findNumberOfTerms(1, red), findNumberOfTerms(2, red)
	return max(min(blueLayer1*2-1, redLayer2*2), min(blueLayer2*2, redLayer1*2-1)) + 1
}

// 定义求解等差数列项数的方法
func findNumberOfTerms(a, Sn int) int {
	// 等差数列求和公式: Sn = (n / 2) * (2a + (n - 1) * b)
	// 我们需要解出 n, 根据公式重写为二次方程：
	// n^2 * b + n * (2a - b) - 2 * Sn = 0
	// n^2 * 2 + n * (2a - 2) - 2 * Sn = 0
	// n^2 + n * (a - 1) - Sn = 0

	// 计算二次方程的系数
	A := float64(1)
	B := float64(a - 1)
	C := float64(-Sn)

	// 使用求解二次方程的公式：n = (-B ± sqrt(B^2 - 4AC)) / 2A
	discriminant := B*B - 4*A*C

	// 计算两个根
	n1 := (-B + math.Sqrt(discriminant)) / (2 * A)
	// n2 := (-B - math.Sqrt(discriminant)) / (2 * A) 必为负数，舍弃

	// 我们只需要正整数解
	return int(n1)
}

复杂度：

• 时间复杂度：O(1)
• 空间复杂度：O(1)

执行结果：

• 执行耗时:3 ms,击败了27.87% 的Go用户
• 内存消耗:2.2 MB,击败了95.08% 的Go用户