1217. 玩筹码
题目描述:
有 n 个筹码。第 i 个筹码的位置是 position[i] 。
我们需要把所有筹码移到同一个位置。在一步中,我们可以将第 i 个筹码的位置从 position[i] 改变为:
- position[i] + 2 或 position[i] - 2 ,此时 cost = 0
- position[i] + 1 或 position[i] - 1 ,此时 cost = 1
返回将所有筹码移动到同一位置上所需要的 最小代价 。
测试用例:
示例1 :
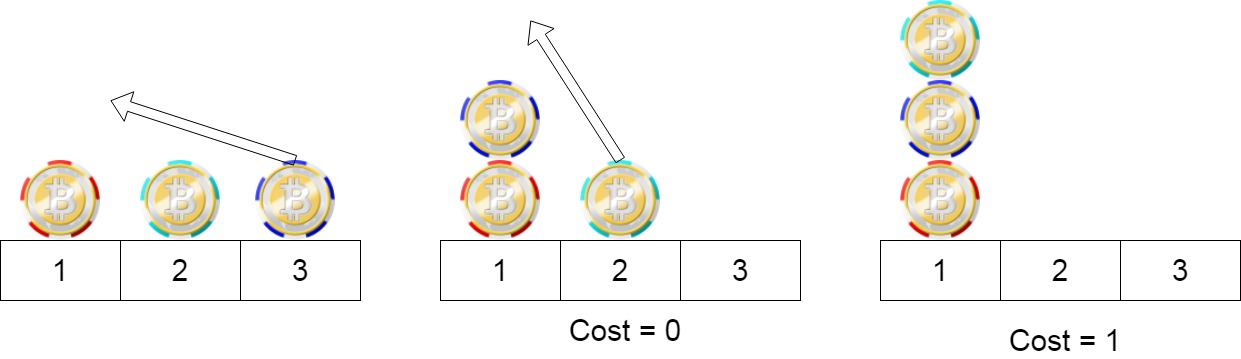
输入:position = [1,2,3]
输出:1
解释:第一步:将位置3的筹码移动到位置1,成本为0。
第二步:将位置2的筹码移动到位置1,成本= 1。
总成本是1。
示例2 :
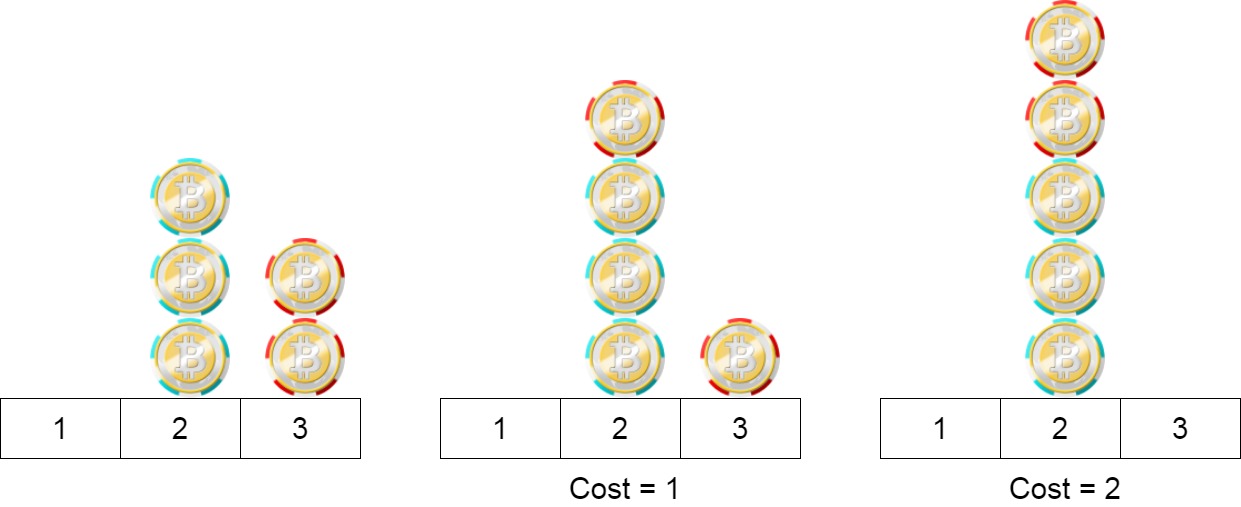
输入:position = [2,2,2,3,3]
输出:2
解释:我们可以把位置3的两个筹码移到位置2。每一步的成本为1。总成本= 2。
示例3 :
输入:position = [1,1000000000]
输出:1
限制及提示:
- 1 <= chips.length <= 100
- 1 <= chips[i] <= 10^9
解题分析及思路:
这一题咋一看怎么这么复杂,一点也不算一道简单题,其实,将它看透其实是真的很简单。
首先不要被题目迷惑,这是一个数组,肯定要想着在这个数组放在某个位置最优解,这样免不了要对整个数组的所有位置摆放进行遍历,但是这样的效果并不好。
其实从结果出发,对于这道题更加简单。
对于他的移动有两种方法和结果:
- position[i] + 2 或 position[i] - 2 ,此时 cost = 0
- position[i] + 1 或 position[i] - 1 ,此时 cost = 1
对于第一种,花费为0,那么对于任意位置的值,只要移动两个,那么它最后结果的影响其实是不变的。
就好比,示例一中,将3位置的筹码放到下标为1的位置,其实对结果是不影响的。
以此类推,是不是可以将所以的结果往前移动n次2个单元,那么所有的数值都会保存在下标为0和1的位置。
然后将下标为0或1的最小的值移到另一个位置就是最优解。
最终的结果就是下标为0和1中的最小值即为最后结果
代码分析:
定义长度为2的数组,将所有筹码往前移动位置,分别放入到数组中。
var ints [2]int
for index := range position {
ints[position[index]%2]++
}
返回最后结果
if ints[0] > ints[1] {
return ints[1]
}
return ints[0]
func minCostToMoveChips(position []int) int {
var ints [2]int
for index := range position {
ints[position[index]%2]++
}
if ints[0] > ints[1] {
return ints[1]
}
return ints[0]
}
复杂度:
- 时间复杂度:O(n),遍历
position所需时间 - 空间复杂度:O(1),存放二维数组所需空间,为常量
执行结果:
- 执行用时: 0 ms , 在所有 Go 提交中击败了 100.00% 的用户
- 内存消耗: 2 MB , 在所有 Go 提交中击败了 100.00% 的用户
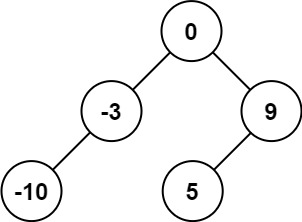 ```
输入:nums = [-10,-3,0,5,9]
输出:
```
输入:nums = [-10,-3,0,5,9]
输出: