303. 区域和检索-数组不可变
题目描述:
给定一个整数数组 nums,处理以下类型的多个查询:
计算索引 left 和 right (包含 left 和 right)之间的 nums 元素的 和 ,其中 left <= right
实现 NumArray 类:
-
NumArray(int[] nums) 使用数组 nums 初始化对象
-
int sumRange(int i, int j) 返回数组 nums 中索引 left 和 right 之间的元素的 总和 ,包含 left 和 right 两点(也就是 nums[left] + nums[left + 1] + … + nums[right] )
测试用例:
示例 1:
输入:
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出:
[null, 1, -1, -3]
解释:
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))
限制及提示:
- 1 <= nums.length <= 10^4
- -10^5 <= nums[i] <= 10^5
- 0 <= i <= j < nums.length
- 最多调用 10^4 次 sumRange 方法
解题分析及思路:
方法一:二叉索引树
该题直接用暴力每次计算left到right之间值的和即可,但是也可以使用树状数组来进行解答。
首先建立一棵二叉索引树。
func Constructor(nums []int) NumArray {
l := len(nums)
ints := make([]int, l+1)
for index := 1; index <= l; index++ {
index1 := index
for index1 <= l {
ints[index1] += nums[index-1]
index1 += lowBit(index1)
}
}
return NumArray{
ints,
}
}
然后每次计算的两个区间的值的时候,计算sum(right + 1) - sum(left)即可。
func sum(ints []int, index int) (ans int) {
for index > 0 {
ans += ints[index]
index -= lowBit(index)
}
return ans
}
复杂度:
- 时间复杂度:
- 初始化O(logN)
- 检索O(1)
- 空间复杂度:O(N)
执行结果:
- 执行用时:24 ms, 在所有 Go 提交中击败了82.00%的用户
- 内存消耗:9.8 MB, 在所有 Go 提交中击败了21.91%的用户
方法二:前缀和
对于计算[left,right]区间的和,我们可以理解为[0,right]区间的和减去[0,left-1]区间的和。
所以可以通过前缀和的方式进行解答:
- 首先,我们可以用一个数组 sums 记录数组 nums 的前缀和.
- 然后,对于检索操作,我们可以通过 sums[right] - sums[left-1] 得到区间和。
只需注意:
- 初始化sums时,首先需要对nums[0]进行初始化。
- 检索时,需要判断left是否为0,如果是0,则直接返回sums[right],因为 0 - 1会越界。
type NumArray struct {
sums []int
}
func Constructor(nums []int) NumArray {
var sums = []int{
nums[0],
}
for i := 1; i < len(nums); i++ {
sums = append(sums, sums[i-1]+nums[i])
}
return NumArray{sums: sums}
}
func (this *NumArray) SumRange(left int, right int) int {
if left == 0 {
return this.sums[right]
}
return this.sums[right] - this.sums[left-1]
}
复杂度:
- 时间复杂度:
- 初始化O(N)
- 检索O(1)
- 空间复杂度:O(N)
执行结果:
- 执行用时:21 ms, 在所有 Go 提交中击败了60.07%的用户
- 内存消耗:9.03 MB, 在所有 Go 提交中击败了97.03%的用户
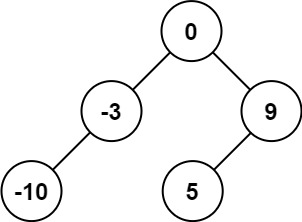 ```
输入:nums = [-10,-3,0,5,9]
输出:
```
输入:nums = [-10,-3,0,5,9]
输出: