766. 托普利茨矩阵
题目描述:
给你一个 m x n 的矩阵 matrix 。如果这个矩阵是托普利茨矩阵,返回 true ;否则,返回 false 。
如果矩阵上每一条由左上到右下的对角线上的元素都相同,那么这个矩阵是 托普利茨矩阵 。
示例 1:
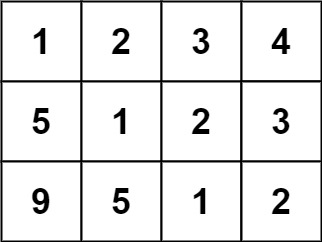
输入:matrix = [[1,2,3,4],[5,1,2,3],[9,5,1,2]]
输出:true
解释:
在上述矩阵中, 其对角线为:
"[9]", "[5, 5]", "[1, 1, 1]", "[2, 2, 2]", "[3, 3]", "[4]"。
各条对角线上的所有元素均相同, 因此答案是 True 。
示例 2:
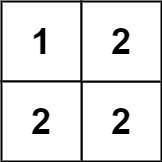
输入:matrix = [[1,2],[2,2]]
输出:false
解释:
对角线 "[1, 2]" 上的元素不同。
提示:
m == matrix.lengthn == matrix[i].length1 <= m, n <= 200 <= matrix[i][j] <= 99
进阶:
- 如果矩阵存储在磁盘上,并且内存有限,以至于一次最多只能将矩阵的一行加载到内存中,该怎么办?
- 如果矩阵太大,以至于一次只能将不完整的一行加载到内存中,该怎么办?
解题分析及思路:
方法:模拟
思路:
以对角线的形式遍历数组,判断左上角到右下角对角线上的元素是否相等。
首先从左上角作为起点开始:
- 首先以每一行的第一个元素作为起点,依次往右下角遍历,判断对角线上的元素是否相等,如果相等,则继续遍历。
- 再以每一列的第一个元素作为起点,依次往右下角遍历,判断对角线上的元素是否相等,如果相等,则继续遍历。
例如:

以1 为起点,以右下角为终点,判断对角线上的元素是否相等,如果相等,则继续遍历。
以5 为起点,以右下角为终点,判断对角线上的元素是否相等,如果相等,则继续遍历。
以9 为起点,以右下角为终点,判断对角线上的元素是否相等,如果相等,则继续遍历。
此时横坐标的遍历完毕,此时纵坐标的遍历还没有结束,此时以纵坐标为起点,以右下角为终点,判断对角线上的元素是否相等,如果相等,则继续遍历。
以2 为起点,以右下角为终点,判断对角线上的元素是否相等,如果相等,则继续遍历。
以3 为起点,以右下角为终点,判断对角线上的元素是否相等,如果相等,则继续遍历。
以4 为起点,以右下角为终点,判断对角线上的元素是否相等,如果相等,则继续遍历。
此时纵坐标的遍历完毕,若所有都满足,则返回true,否则返回false。
func isToeplitzMatrix(matrix [][]int) bool {
validate := func(row, col int) bool {
for row < len(matrix)-1 && col < len(matrix[0])-1 {
if matrix[row][col] != matrix[row+1][col+1] {
return false
}
row++
col++
}
return true
}
for i := 0; i < len(matrix); i++ {
if !validate(i, 0) {
return false
}
}
for i := 1; i < len(matrix[0]); i++ {
if !validate(0, i) {
return false
}
}
return true
}
复杂度:
- 时间复杂度:O(n * m)
- 空间复杂度:O(1)
执行结果:
- 执行耗时:5 ms,击败了79.17% 的Go用户
- 内存消耗:3.6 MB,击败了87.50% 的Go用户
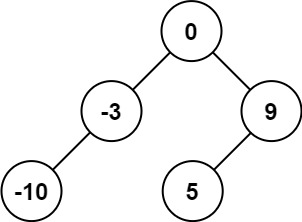 ```
输入:nums = [-10,-3,0,5,9]
输出:
```
输入:nums = [-10,-3,0,5,9]
输出: