98. 验证二叉搜索树
题目描述:
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左子树只包含 小于 当前节点的数。
- 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
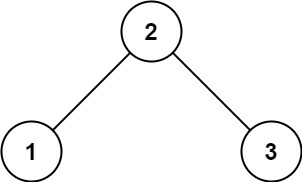
输入:root = [2,1,3]
输出:true
示例 2:

输入:root = [5,1,4,null,null,3,6]
输出:false
解释:根节点的值是 5 ,但是右子节点的值是 4 。
提示:
- 树中节点数目范围在[1, 10^4] 内
- -2^31 <= Node.val <= 2^31 - 1
解题分析及思路:
这道题考察的是二叉树的遍历,不熟悉二叉树的遍历可以查看二叉树。
这道题有关二叉搜索树
方法一:中序遍历
由于二叉搜索树的中序遍历本身就是一个递增的序列,所以可以通过中序遍历的方式来解决。
所以我们仅仅需要遍历一次二叉搜索树,然后将遍历的结果保存在一个数组中,然后判断数组是否是递增的即可。
func isValidBST(root *TreeNode) bool {
var nums []int
var dfs func(node *TreeNode)
dfs = func(node *TreeNode) {
if node == nil {
return
}
dfs(node.Left)
nums = append(nums, node.Val)
dfs(node.Right)
}
dfs(root)
for i := 1; i < len(nums); i++ {
if nums[i] <= nums[i-1] {
return false
}
}
return true
}
复杂度:
- 时间复杂度:O(N),其中 N 是树中的节点个数
- 空间复杂度:O(N),其中 N 是树中的节点个数
执行结果:
- 执行耗时:3 ms,击败了86.13% 的Go用户
- 内存消耗:6.1 MB,击败了7.58% 的Go用户
方法二:递归
我们可以通过递归的方式来解决这个问题,我们可以定义一个递归函数来判断当前节点是否是一个有效的二叉搜索树。
可以判断每个节点的左子树的最大值是否小于当前节点的值,右子树的最小值是否大于当前节点的值。
但是这样存在一个问题,那就是当右子树的左节点的值小于当前节点的值,这样就会导致右子树的最小值小于当前节点的值,所以我们需要引入一个最小值和最大值来解决这个问题。
- 当遍历左子树时,我们需要将当前节点的值作为最大值传递给左子树
- 当遍历右子树时,我们需要将当前节点的值作为最小值传递给右子树
func isValidBST(root *TreeNode) bool {
var helper func(node *TreeNode, min *TreeNode, max *TreeNode) bool
helper = func(node *TreeNode, min *TreeNode, max *TreeNode) bool {
if node == nil {
return true
}
if min != nil && node.Val <= min.Val {
return false
}
if max != nil && node.Val >= max.Val {
return false
}
return helper(node.Left, min, node) && helper(node.Right, node, max)
}
return helper(root, nil, nil)
}
复杂度:
- 时间复杂度:O(N),其中 N 是树中的节点个数
- 空间复杂度:O(1
执行结果:
- 执行耗时:3 ms,击败了86.13% 的Go用户
- 内存消耗:5.2 MB,击败了68.72% 的Go用户
 ```
输入: preorder = [3,9,20,15,7], inorder = [
```
输入: preorder = [3,9,20,15,7], inorder = [ ```
输入:inorder = [9,3,15,20,7], postorder
```
输入:inorder = [9,3,15,20,7], postorder  ```
输入: head = [-10,-3,0,5,9]
输出: [0,-3,9
```
输入: head = [-10,-3,0,5,9]
输出: [0,-3,9 ```
输入:root
```
输入:root