563. 二叉树的坡度

题目描述：

给你一个二叉树的根节点 root ，计算并返回 整个树 的坡度 。

一个树的 节点的坡度 定义即为，该节点左子树的节点之和和右子树节点之和的 差的绝对值 。如果没有左子树的话，左子树的节点之和为 0 ；没有右子树的话也是一样。空结点的坡度是 0 。

整个树 的坡度就是其所有节点的坡度之和。

示例 1：

输入：root = [1,2,3]
输出：1
解释：
节点 2 的坡度：|0-0| = 0（没有子节点）
节点 3 的坡度：|0-0| = 0（没有子节点）
节点 1 的坡度：|2-3| = 1（左子树就是左子节点，所以和是 2 ；右子树就是右子节点，所以和是 3 ）
坡度总和：0 + 0 + 1 = 1

示例 2：

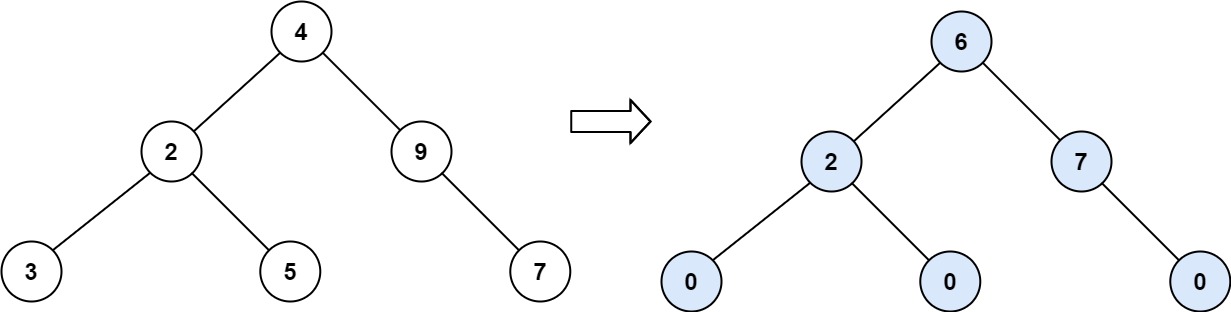
输入：root = [4,2,9,3,5,null,7]
输出：15
解释：
节点 3 的坡度：|0-0| = 0（没有子节点）
节点 5 的坡度：|0-0| = 0（没有子节点）
节点 7 的坡度：|0-0| = 0（没有子节点）
节点 2 的坡度：|3-5| = 2（左子树就是左子节点，所以和是 3 ；右子树就是右子节点，所以和是 5 ）
节点 9 的坡度：|0-7| = 7（没有左子树，所以和是 0 ；右子树正好是右子节点，所以和是 7 ）
节点 4 的坡度：|(3+5+2)-(9+7)| = |10-16| = 6（左子树值为 3、5 和 2 ，和是 10 ；右子树值为 9 和 7 ，和是 16 ）
坡度总和：0 + 0 + 0 + 2 + 7 + 6 = 15

示例 3：

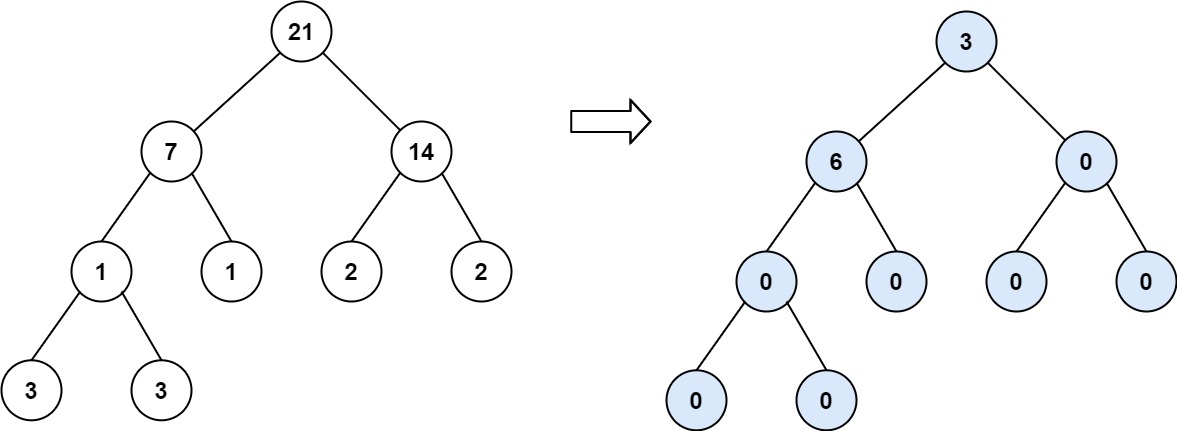
输入：root = [21,7,14,1,1,2,2,3,3]
输出：9

提示：

• 树中节点数目的范围在 [0, 10^4] 内
• -1000 <= Node.val <= 1000

---

解题分析及思路：

方法：深度优先搜索

这道题考察的是二叉树的遍历，不熟悉二叉树的遍历可以查看二叉树。

题目要求我们计算整个树的坡度，我们可以使用深度优先搜索的方法，计算每个节点的坡度，然后累加起来。

我们可以使用一个递归函数 dfs，计算每个节点的坡度，然后累加起来。dfs 函数的返回值是以 node 为根的子树的节点之和。

在 dfs 函数中：

• 首先递归计算左子树的节点之和 leftValue
• 然后递归计算右子树的节点之和 rightValue
• 计算以 node 为根的子树的坡度，即 abs(leftValue - rightValue)，并累加到 sum 中。
• 最后，我们返回以 node 为根的子树的节点之和 node.Val + leftValue + rightValue。

最后，我们返回 sum 即可。

func findTilt(root *TreeNode) int {
	var sum int
	var dfs func(node *TreeNode) int
	dfs = func(node *TreeNode) int {
		if node == nil {
			return 0
		}
		var leftValue = dfs(node.Left)
		var rightValue = dfs(node.Right)
		if leftValue < rightValue {
			sum += rightValue - leftValue
		} else {
			sum += leftValue - rightValue
		}
		return node.Val + leftValue + rightValue
	}
	dfs(root)
	return sum
}

复杂度：

• 时间复杂度：O(N)，其中 N 是树中的节点个数.
• 空间复杂度：O(1)，只使用常数额外空间。

执行结果：

• 执行耗时:4 ms,击败了92.86% 的Go用户
• 内存消耗:6.1 MB,击败了83.33% 的Go用户