993. 二叉树的堂兄弟节点
题目描述:
在二叉树中,根节点位于深度 0 处,每个深度为 k 的节点的子节点位于深度 k+1 处。
如果二叉树的两个节点深度相同,但 父节点不同 ,则它们是一对堂兄弟节点。
我们给出了具有唯一值的二叉树的根节点 root ,以及树中两个不同节点的值 x 和 y 。
只有与值 x 和 y 对应的节点是堂兄弟节点时,才返回 true 。否则,返回 false。
示例 1:
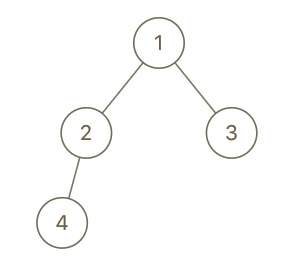
输入:root = [1,2,3,4], x = 4, y = 3
输出:false
示例 2:
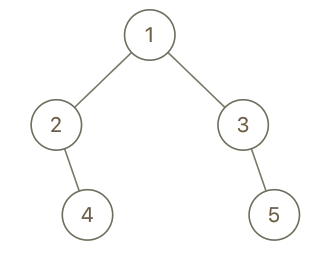
输入:root = [1,2,3,null,4,null,5], x = 5, y = 4
输出:true
示例 3:

输入:root = [1,2,3,null,4], x = 2, y = 3
输出:false
提示:
- 二叉树的节点数介于 2 到 100 之间。
- 每个节点的值都是唯一的、范围为 1 到 100 的整数。
解题分析及思路:
这道题考察的是二叉树的遍历,不熟悉二叉树的遍历可以查看二叉树。
方法:广度优先遍历
可以使用广度优先搜索的方法,遍历整个二叉树,对于每一层的节点,如果存在x,并且y,并且它们的父节点不为同一节点,则为一对堂兄弟节点。
func isCousins(root *TreeNode, x int, y int) bool {
queue := []*TreeNode{root}
for len(queue) != 0 {
var queue1 []*TreeNode
var flagX, flagY = false, false
for index := range queue {
if (queue[index].Left != nil && queue[index].Right != nil) && ((queue[index].Left.Val == x && queue[index].Right.Val == y) ||
(queue[index].Left.Val == y && queue[index].Right.Val == x)) {
return false
}
if queue[index].Left != nil {
queue1 = append(queue1, queue[index].Left)
}
if queue[index].Right != nil {
queue1 = append(queue1, queue[index].Right)
}
if x == queue[index].Val {
flagX = true
}
if y == queue[index].Val {
flagY = true
}
}
if flagX && flagY {
return true
}
queue = queue1
}
return false
}
复杂度:
- 时间复杂度:O(N),其中 N 是树中的节点个数
- 空间复杂度:O(N),其中 N 是树中的节点个数
执行结果:
- 执行耗时:2 ms,击败了12.28% 的Go用户
- 内存消耗:2.3 MB,击败了36.85% 的Go用户
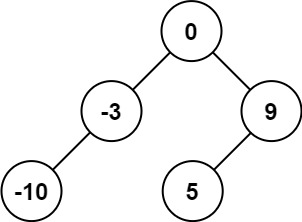 ```
输入:nums = [-10,-3,0,5,9]
输出:
```
输入:nums = [-10,-3,0,5,9]
输出: