543. 二叉树的直径
题目描述:
给你一棵二叉树的根节点,返回该树的 直径 。
二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。
两节点之间路径的 长度 由它们之间边数表示。
示例 1:
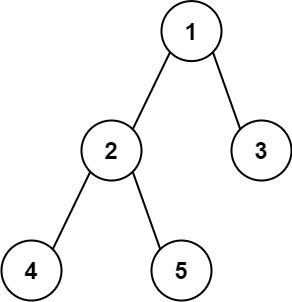
输入:root = [1,2,3,4,5]
输出:3
解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
示例 2:
输入:root = [1,2]
输出:1
提示:
- 树中节点数目在范围 [1, 10^4] 内
- -100 <= Node.val <= 100
解题分析及思路:
这道题考察的是二叉树的遍历,不熟悉二叉树的遍历可以查看二叉树。
方法:分治法
二叉树的直径是指树中任意两个节点之间最长路径的长度。
这条路径可能经过也可能 不经过根节点 root 。
重点在于答案可能不经过根节点,这也是很容易出错的地方。
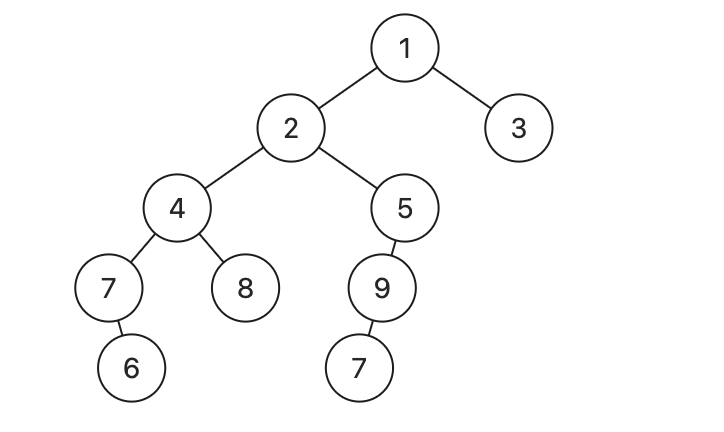
例如:[1,2,3,4,5,null,null,7,8,9,null,null,6,null,null,7]
他的答案并不是[6,7,4,2,1,3],而是[6,7,4,2,5,9,7],后者长度比前者更加长。
所以,我们可以考虑使用深度优先搜索和分治法,对于每一个节点,我们可以计算该节点的左右子树的最大深度,然后计算该节点的直径,最后取最大值。
对于节点 root,其直径为 getMaxDiameter(root.Left) + getMaxDiameter(root.Right) + 1。
func diameterOfBinaryTree(root *TreeNode) int {
var ans = 1
getMaxDiameter(root, &ans)
return ans - 1
}
func getMaxDiameter(root *TreeNode, ans *int) int {
if root == nil {
return 0
}
left := getMaxDiameter(root.Left, ans)
right := getMaxDiameter(root.Right, ans)
*ans = max(*ans, left+right+1)
return max(left, right) + 1
}
func max(i, j int) int {
if i > j {
return i
}
return j
}
复杂度:
- 时间复杂度:O(N),其中 N 是树中的节点个数
- 空间复杂度:O(1)
执行结果:
- 执行耗时:0 ms,击败了100.00% 的Go用户
- 内存消耗:4.4 MB,击败了80.62% 的Go用户
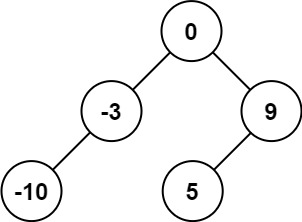 ```
输入:nums = [-10,-3,0,5,9]
输出:
```
输入:nums = [-10,-3,0,5,9]
输出: